Рациональной дробью 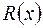 называется функция, равная отношению двух многочленов:
называется функция, равная отношению двух многочленов:
 ,
,
где, m, n – целые положительные числа, 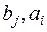 - действительные числа (
- действительные числа (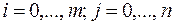 ).
).
Если 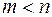 , то
, то 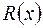 называется правильной рациональной дробью, если
называется правильной рациональной дробью, если 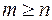 - неправильной дробью.
- неправильной дробью.
Всякую неправильную дробь путем деления 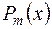 на
на 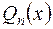 можно представить в виде суммы некоторого многочлена и правильной дроби.
можно представить в виде суммы некоторого многочлена и правильной дроби.
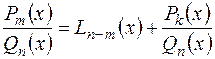 ,
,
где 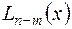 ,
,  - многочлены;
- многочлены; 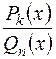 - правильная рациональная дробь
- правильная рациональная дробь 
Интегрирование правильной рациональной дроби основано на следующей теории.
Каждая правильная рациональная дробь может быть представлена в виде суммы конечного числа простейших дробей следующих четырех видов:
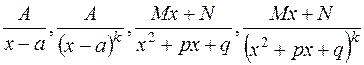
где, A, a, M, N, p, q – действительные числа, k – натуральное число 
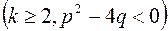 .
.
В алгебре устанавливается, что если знаменатель дроби представить в виде:
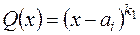
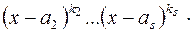

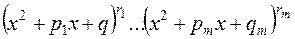 ,
,
то в разложении самой дроби:
а) каждому множителю вида  соответствует одна простейшая дробь вида
соответствует одна простейшая дробь вида 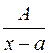 ;
;
б) каждому множителю вида 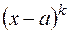 соответствует сумма простейших дробей вида:
соответствует сумма простейших дробей вида: 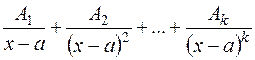 ;
;
в) каждому множителю 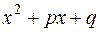 соответствует одна простейшая дробь вида
соответствует одна простейшая дробь вида 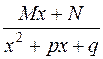 .
.
Пример12. Найти интеграл 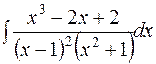 .
.
Решение. Разложим правильную рациональную дробь на сумму простейших дробей:
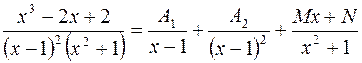 .
.
Приводя дроби к общему знаменателю и приравнивая числители, получим:
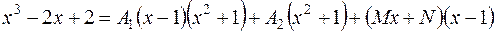
Так как данное тождество должно выполняться для любого 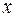 , то зададим аргументу значение
, то зададим аргументу значение  и получим
и получим 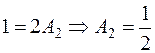 .
.
Сравнивая коэффициенты при одинаковых степенях 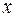 в тождестве, находим:
в тождестве, находим:
При 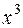 :
: 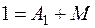
При 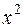 :
: 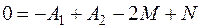
При 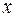 :
: 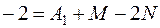
При 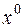 :
: 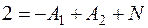
Подставив значение 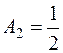 , находим:
, находим: 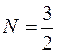 ,
, 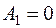 ,
, 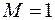 .
.
Поэтому:

Вычислить неопределенные интегралы.
5.1 
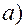
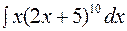
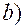
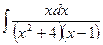
5.2 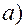
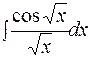
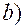
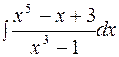 .
.
5. 
3 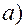
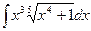
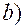
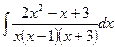 .
.
5. 
4 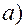
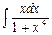
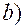
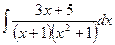 .
.
5. 
5 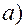
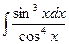
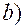
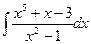 .
.
5. 
6 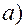
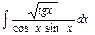
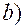
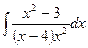 .
.
5. 
7 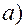
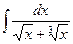
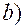
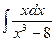 .
.
5. 
8 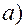
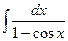
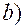
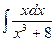 .
.
5. 
9 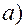

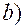
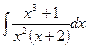 .
.
5. 
10 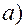
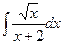
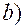
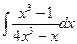 .
.
5. 
11 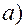
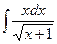
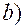
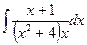 .
.
5.12 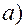
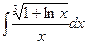
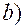
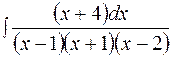 .
.
5.13 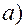
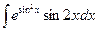
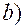
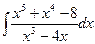 .
.
5.14 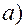
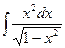
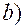
 .
.
5.15 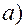
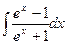
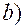
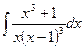 .
.
5.16 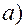
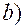
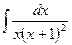 .
.
5.17 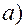
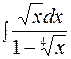
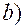
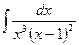 .
.
5.18 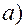
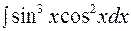
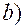
 .
.
5.19 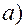
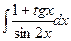
 .
.
5.20 
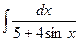
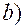
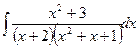 .
.
 2015-10-22
2015-10-22 2216
2216
