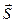2015-10-22
2338
Скалярным полем называется часть пространства (или все пространство), каждой точке которой соответствует численное значение некоторой скалярной величины.
Примеры
Тело, имеющее в каждой точке определенное значение температуры – скалярное поле.
Неоднородное тело, каждой точке которой соответствует определенная плотность – скалярное поле плотности.
Во всех этих случаях скалярная величина U не зависит от времени, а зависит от положения (координат) точки М в пространстве, то есть 
-- это функция трех переменных, она называется функцией поля. И обратно, всякая функция трех переменных u=f(x, y, z) задает некоторое скалярное поле.
Функция плоского скалярного поля зависит от двух переменных z=f(x, y).
Рассмотрим скалярное поле u=f(x, y, z).
Вектор, координатами которого являются частные производные функции, вычисленные в заданной точке, называется градиентом функции в этой точке.
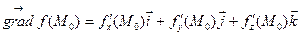
или
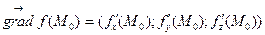
Рассмотрим некоторый вектор 
и на нем две точки M0(x0, y0, z0) и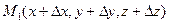 
. Найдем приращение функции в направлении :
.
Производной по направлению называется следующий предел, если он существует:
.
где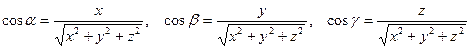 
-- направляющие косинусы вектора ; α, β, γ -- углы, которые образует вектор с осями координат.
Для функции двух переменных эти формулы принимают вид:
|
или 
,
|
так как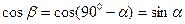 
.  |
Между градиентом и производной по направлению в одной и той же точке существует связь.
Теорема. Скалярное произведение градиента функции на вектор некоторого направления равно производной данной функции в направлении этого вектора:
.
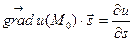Следствие. Производная по направлению имеет наибольшее значение, если это направление совпадает с направлением градиента (обосновать самостоятельно, используя определение скалярного произведения и считая, что 
).
Выводы:
1. Градиент – это вектор, показывающий направление наибольшего возрастания функции в данной точке и имеющий модуль, численно равный скорости этого возрастания:
.
2. Производная по направлению – это скорость изменения функции в направлении : если 
, то функция в этом направлении возрастает,
если 
, то функция убывает.
3. Если вектор совпадает с одним из векторов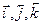 
, то производная по направлению этого вектора совпадает с соответствующей частной производной.
Например, если 
, тогда 
.
Пример (см. задание VII)
Даны функция 
, точка А(1, 2) и вектор 
.
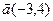Найти: 1) 
;
2) 
.
Решение.
1) найдем частные производные функции и вычислим их в точке А.
, 
.
Тогда 
.
2) Найдем направляющие косинусы вектора :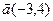
.
Тогда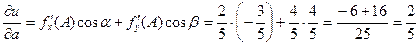 
.
Ответ: ;
.
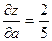Ниже приведены задания для контрольной работы.
Номер варианта соответствует последней цифре Вашего шифра. Из каждого задания необходимо выполнить пример, номер которого совпадает с номером Вашего варианта.
Каждую контрольную работу следует выполнять в отдельной тетради. Следует указать свой шифр и номер варианта. Условие задачи должно быть полностью переписано перед ее решением.
Отмеченные рецензентом ошибки необходимо исправить в конце работы, сделав работу над ошибками.
Зачтенные контрольные работы предъявляются студентом при сдаче зачета или экзамена.
