На практике часто встречаемся с величинами, значения которых зависят от нескольких величин, изменяющихся независимо друг от друга. Рассмотрим простейший случай, когда таких независимых переменных две.
Пусть М – некоторое множество пар 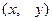 действительных чисел. Функцией двух переменных называется правило (закон), по которому каждой паре чисел
действительных чисел. Функцией двух переменных называется правило (закон), по которому каждой паре чисел 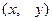
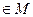 ставится в соответствие единственное число
ставится в соответствие единственное число 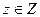 , при условии, что каждое
, при условии, что каждое 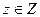 соответствует хотя бы одной паре
соответствует хотя бы одной паре 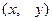
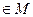 .
.
x,y – независимые переменные;
М – область определения;
Z – область значений;
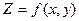
Так как каждой паре 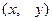 соответствует единственная точка P(x, y) и обратно, то функцию двух переменных можно рассматривать как функцию точки Р.
соответствует единственная точка P(x, y) и обратно, то функцию двух переменных можно рассматривать как функцию точки Р.
Если функция двух переменных задана с помощью аналитического выражения (формулы) без каких-либо дополнительных условий относительно области определения, то областью определения принято считать множество таких точек плоскости Оxy (пар 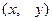 ), для которых это аналитическое выражение имеет смысл и дает действительное значение функции.
), для которых это аналитическое выражение имеет смысл и дает действительное значение функции.
Пример: функция 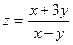 определена для всех точек
определена для всех точек 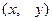 плоскости Оxy, кроме точек прямой x-y=0.
плоскости Оxy, кроме точек прямой x-y=0.
Рассмотрим функцию двух переменных 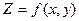 . Зафиксируем одну из переменных, например, пусть
. Зафиксируем одну из переменных, например, пусть  . Тогда
. Тогда 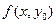 -- функция одной переменной х.
-- функция одной переменной х.
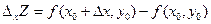 -- частное приращение функции
-- частное приращение функции 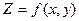 по переменной х.
по переменной х.
Аналогично, если зафиксируем х=х0, то
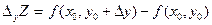 -- частное приращение функции
-- частное приращение функции 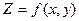 по переменной y.
по переменной y.
Если существуют конечные пределы, то:
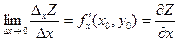 --
--
называется частной производной по х (или частной производной первого порядка);
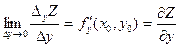 --
--
называется частной производной по y.
Выводы:
1. Частная производная функции двух переменных по одному из ее аргументов равна пределу отношения частного приращения функции к вызвавшему это приращение аргументу, когда приращение аргумента стремится к нулю.
2. Частные производные в точке (x0, y0) – это числа, зависящие от координат точки, в которой вычисляются, то есть в общем случае это функция двух переменных.
3. Частная производная определяется как производная функции одной переменной (другую переменную фиксировали), поэтому для частных производных справедливы все правила и формулы дифференцирования функции одной переменной. Следует помнить, что при нахождении частной производной какому-либо аргументу, все аргументы считаются постоянными.
Примеры
1) 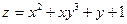 ;
;
 .
.
2) 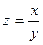 ;
;
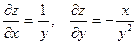 .
.
 2015-10-22
2015-10-22 1664
1664
