Свойства сходящихся рядов

· Если сходится ряд: , то сходится и ряд: , и обратно. Другими словами на сходимость ряда не влияет отбрасывание любого конечного числа его первых членов.

Сходящиеся ряды можно умножать на число, почленно складывать и вычитать так же, как и конечные суммы:

· Если сходится ряд: 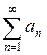и его сумма равна S, то и ряд 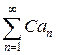где С = const, сходится и его сумма равна СS.

· Если сходятся ряды: 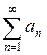и 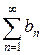и их суммы равны S_а и S_b, то и ряд , сходится и его сумма равна S_а ± S_b.

Необходимое условие сходимости ряда:

Если ряд сходится, то его общий член стремится к нулю, то есть . Данное условие не является достаточным.

Рассмотрим гармонический ряд: и он расходится.

Задание 2. Написать первые пять членов ряда и исследовать ряд на сходимость:

Необходимое условие сходимости ряда выполняется: . Данный ряд является геометрической прогрессией, в которой Так как , то ряд сходится.	Необходимое условие сходимости ряда   _________________: Данный ряд является геометрической прогрессией, в которой   Так как , то ряд ________________.
Необходимое условие сходимости ряда выполняется: . Данный ряд является геометрической прогрессией, в которой Так как , то ряд сходится.	Необходимое условие сходимости ряда   _________________: Данный ряд является геометрической прогрессией, в которой Так как , то ряд _______________.