Функция y=f(x) называется возрастающей в промежутке  , если для любых
, если для любых  и
и  , принадлежащих этому промежутку и таких, что
, принадлежащих этому промежутку и таких, что  <
<  , имеет место неравенство
, имеет место неравенство  .
.
Функция y=f(x) называется убывающей в промежутке  , если для любых
, если для любых  и
и  , принадлежащих этому промежутку и таких, что
, принадлежащих этому промежутку и таких, что  <
<  , имеет место неравенство
, имеет место неравенство  .
.
Как возрастающие, так и убывающие функции называются монотонными, а промежутки, в которых функция возрастает или убывает, - промежутками монотонности.
Возрастание и убывание функции y=f(x) характеризуется знаком её производной.
Теорема
Для того чтобы дифференцируемая на  функция y=f(x) не убывала (не возрастала) на этом интервале, необходимо и достаточно чтобы
функция y=f(x) не убывала (не возрастала) на этом интервале, необходимо и достаточно чтобы  для всех х из этого интервала.
для всех х из этого интервала.
Если же для любого х из 
 то функция y=f(x) монотонно возрастает (монотонно убывает) на этом интервале.
то функция y=f(x) монотонно возрастает (монотонно убывает) на этом интервале.
Из теоремы следует, что для того чтобы функция y=f(x) была постоянной на  , необходимо и достаточно, чтобы выполнялось условие:
, необходимо и достаточно, чтобы выполнялось условие: 
| f´(x)<0 |
| f´(x)=0 |
| f´(x)<0 |
Внутренние точки области определения, в которых производная не существует или равна нулю, называются критическими.
Точка 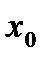 из области определения D(f) точкой максимума (минимума) этой функции, если существует такой интервал
из области определения D(f) точкой максимума (минимума) этой функции, если существует такой интервал  ,
,  , не выходящий из области определения D(f), что для всех х ≠
, не выходящий из области определения D(f), что для всех х ≠ 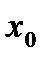 , выполняется неравенство
, выполняется неравенство 
| х0 |
| f(х0) |
| х0 |
| f(х0) |


Точки максимума и минимума функции называются точками экстремума, а значения функции в этих точках – экстремумы функции.
Следующая теорема показывает, что точки экстремума следует искать среди критических точек функции.
Теорема Ферма
Если точка 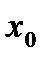 - точка экстремума функции y=f(x) и в этой точке существует производная, то
- точка экстремума функции y=f(x) и в этой точке существует производная, то 
 2015-10-22
2015-10-22 526
526








