Основные теоремы о непрерывных функциях

Функция у=f(x) называется непрерывной в точке 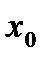, если:

1)функция определена в этой точке;

2)в некоторой окрестности точки 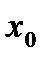существует предел функции в точке 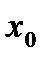, который совпадает со значением функции в этой точке.

Т.е.

При невыполнении одного из этих условий функция терпит разрыв в точке .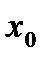

Классификация точек разрыва.

Точка 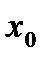называется точкой разрыва I рода функции f(x), если в этой точке существуют конечные пределы справа и слева в точке 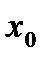, не равные друг другу.

Точка 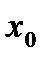называется точкой разрыва II рода функции f(x), если в этой точке правый или левый пределы не существуют или являются бесконечными.

Пример.

Найдите точки разрыва функции f(x) и выясните характер этих точек.

а)

Функция определена на всей числовой прямой. Найдем односторонние пределы в точке 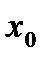=1

,

Односторонние пределы существуют, конечны, но не равны друг другу, следовательно 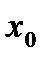=1 – точка разрыва I рода.

б) f(x)=

Функция определена всюду, кроме точки 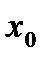= -1, значит 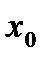= -1 – точка разрыва. Установим какого рода.

,

Значит, 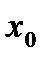= -1 – точка разрыва II рода.

в)

Функция определена всюду, кроме точки 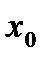= 1, значит 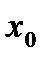= 1 – точка разрыва. Установим какого рода.

,

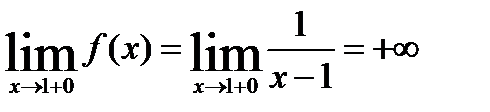
Поскольку односторонние пределы в точке 1 бесконечны, то 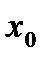= 1 – точка разрыва II рода.

Исследуем функцию в окрестности точки 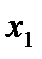= 0

,

Односторонние пределы существуют, конечны, равны друг другу, проверим значение функции в точке 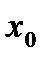=0

f(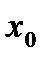)=f(0)=

Значение функции совпадает с односторонними пределами, следовательно, в точке =0 разрыва нет.