Решение типовых примеров

Теория пределов

1. Вычислить пределы функций:

2. Составить уравнения асимптот к графику функции:

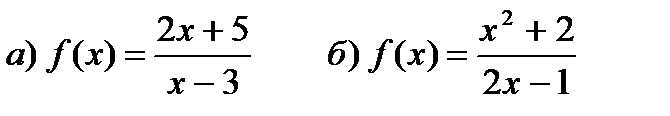
Решение

а) Графики функций могут иметь асимптоты трех видов: горизонтальные, вертикальные и наклонные.

Для определения горизонтальной асимптоты следует вычислить предел функции при условии, что х®¥. Если такой предел существует, то график функции имеет горизонтальную асимптоту.

В примере 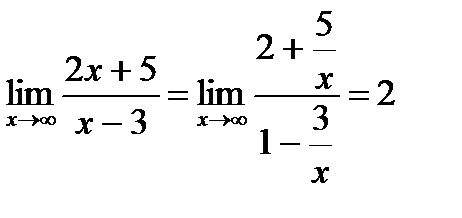График функции имеет горизонтальную асимптоту с уравнением у=2.

Для определения вертикальной асимптоты следует определить значения, при которых функция не существует и найти левые и правые пределы функции. Если хотя бы один из пределов бесконечен, то имеется вертикальная асимптота.

В примере функция не существует при х=3.

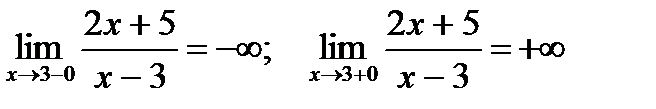Так как оба предела бесконечны, то имеется

вертикальная асимптота с уравнением х=3.

Для определения наклонной асимптоты с уравнением y=kx +b находят

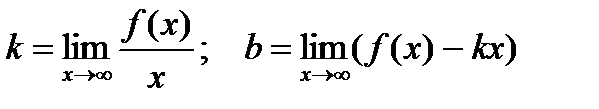Если первый предел не существует или равен 0, то нет наклонной асимптоты.

В примере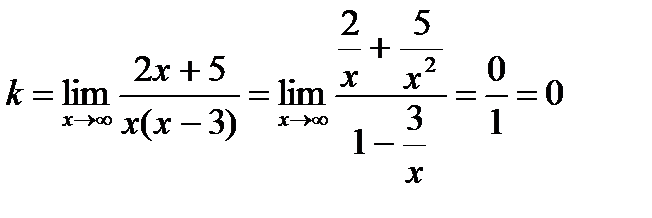

Так как k=0, то наклонной асимптоты не имеется.

б)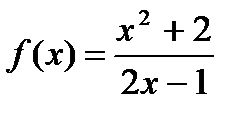

Выполним последовательно значения пределов:

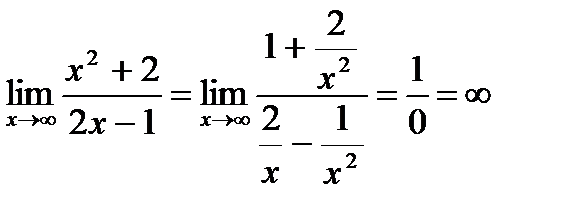График функции не имеет горизонтальной асимптоты.

Функция не существует при х=0,5

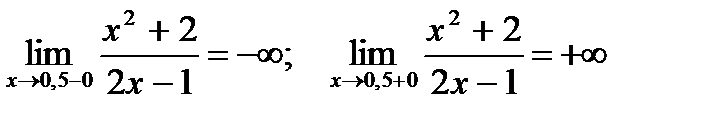График функции имеет вертикальную асимптоту

с уравнением х=0,5

Вычислим 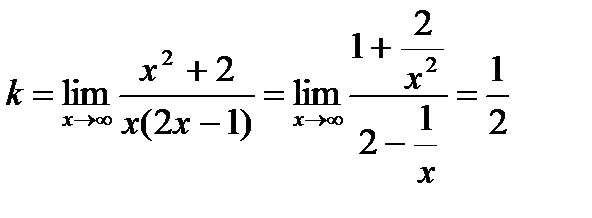График функции имеет наклонную асимптоту.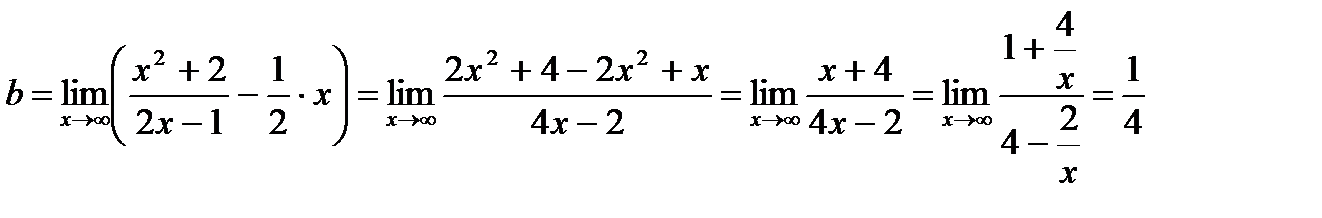

Наклонная асимптота имеет уравнение у=0,5х + 0,25

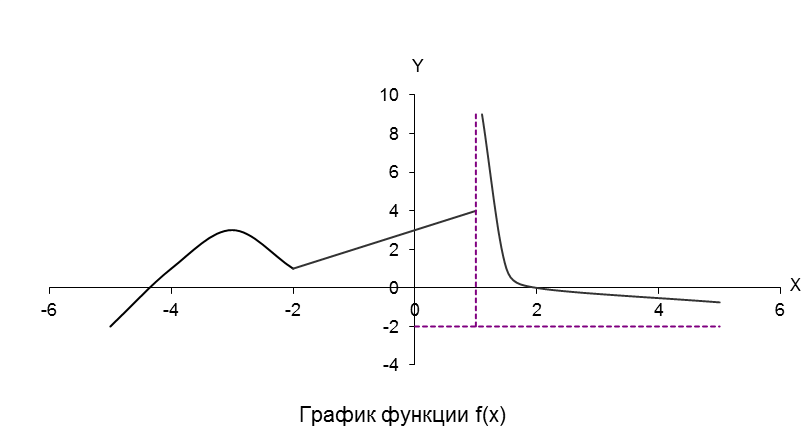
3. Построить график функции, определив тип точек разрыва:

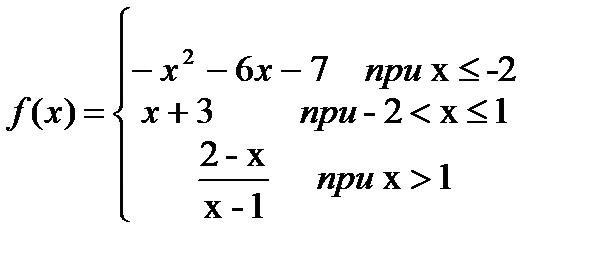
Для заданной функции точками разрыва являются значения аргумента (-2) и 1.

Найдем левые и правые предельные значения функции для этих значений аргумента.

Для построения графика функции с учетом определения типов точек разрыва, потребуется вычисление значений функции в некоторых промежуточных точках

а) x < -2 y=-x²-6x-7 (парабола)

xi	-5	-4	-3	-2
yi	-2

б) -2<x < 1 y=x+3 (прямая)

xi	-2
yi

в) х>1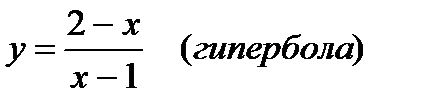

xi	1,1	1,5
yi				-0,75	-0,875

Если вычислить 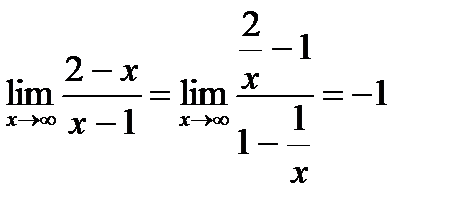, то получим уравнение горизонтальной

асимптоты у=-1

Линейная алгебра

1. Выполнить действия над матрицами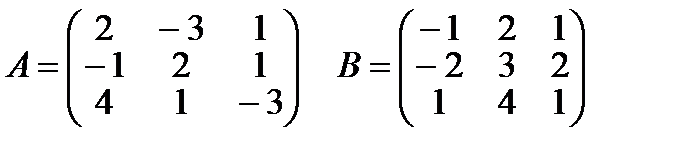

Составить матрицу М=(2А – В)(В+Е)

Решение:

Составим матрицу 2А – В, для чего все элементы матрицы А умножим на 2, а затем из каждого элемента матрицы 2А вычтем соответствующий элемент матрицы В.

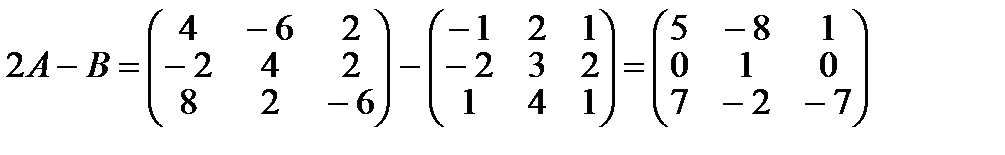
Составим матрицу В+Е, где матрица Е является единичной матрицей третьего порядка:

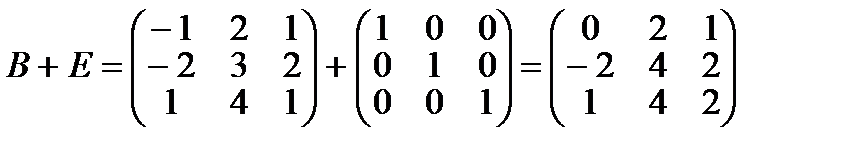
Матрица М является произведением полученных матриц, то есть каждый ее элемент равен сумме произведений соответствующих элементов строки матрицы 2А-В и столбца матрицы В+Е

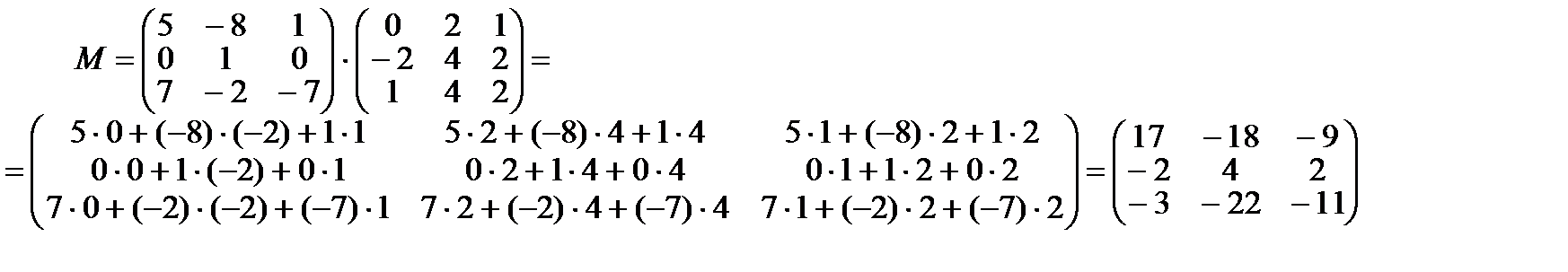
2. Вычислить определитель матрицы:

а)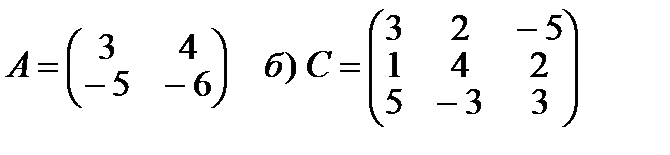

Решение:

а) Для вычисления определителя второго порядка воспользуемся правилом, изложенным в учебной литературе:

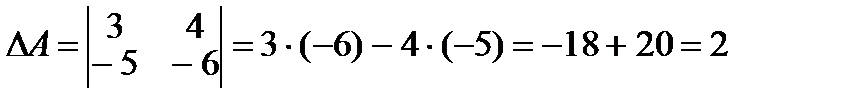
б) Для вычисления определителя третьего порядка воспользуемся одним из правил, называемым разложением по элементам первой строки:

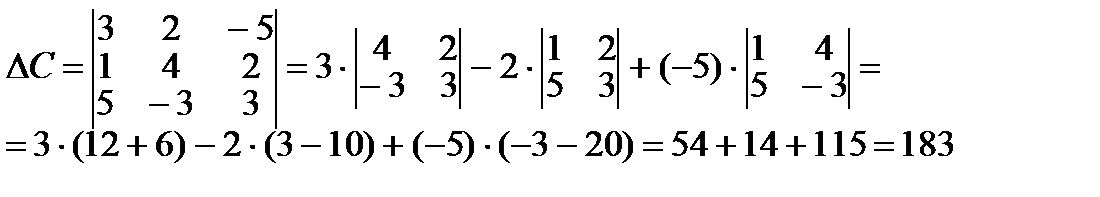
3. Найти обратную матрицу для матрицы второго порядка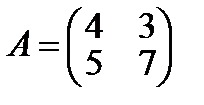

Решение:

Для получения обратной матрицы А^-1 воспользуемся формулой 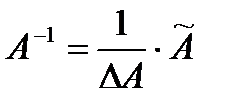, где

Для проверки можно найти произведение матриц А и А^-1; должна получиться единичная матрица второго порядка.

4. Решить систему уравнений по формулам Крамера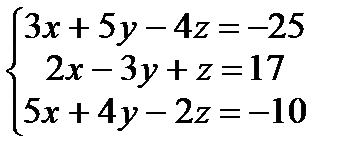

Решение:

Для решения задачи нужно вычислить четыре определителя третьего порядка:

· главный определитель, составленный из коэффициентов при неизвестных;

· дополнительный для х, полученный из главного определителя заменой чисел первого столбца на свободные члены;

· дополнительный для у, полученный из главного определителя заменой чисел второго столбца на свободные члены;

· дополнительный для z, полученный из главного определителя заменой чисел третьего столбца на свободные члены;

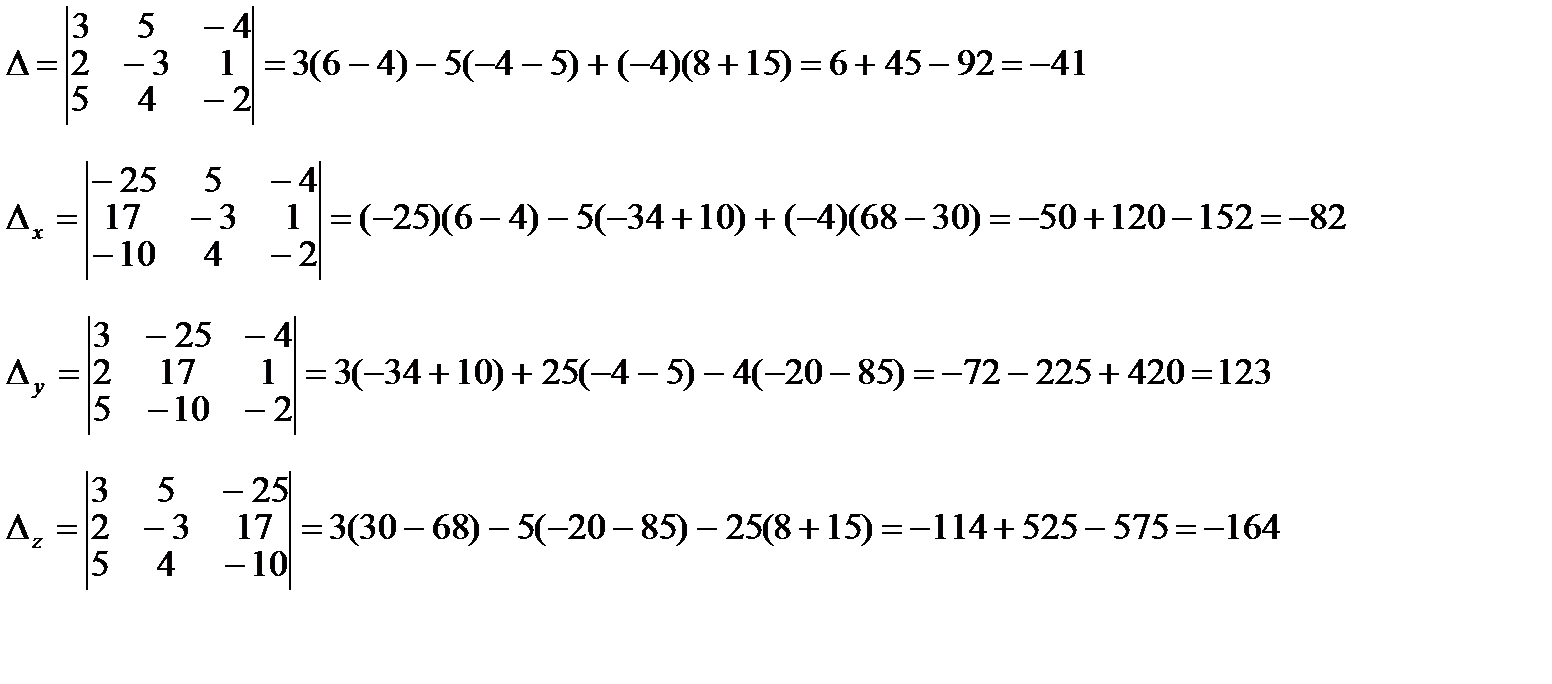
Для получения значений неизвестных требуется разделить значения дополнительных определителей на главный определитель.

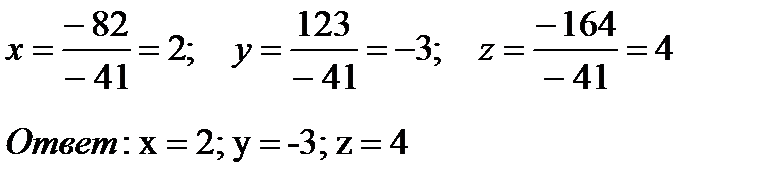
Решение задачи можно проверить при помощи найденных значений в уравнения системы.