1. Найти производные функций:
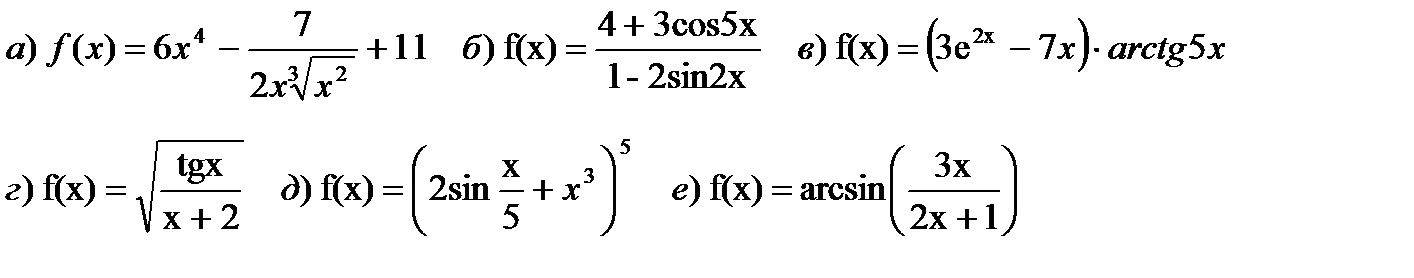
Решение:
При выполнении дифференцирования будем использовать свойства производных, таблицу производных, правило дифференцирования сложных функций.

Исследование функций с помощью производной
1. Выполнить исследование свойств функции по первой и второй производным и построить график функции f(x)=x3 - 3x2 - 45x + 20
Решение
Воспользуемся некоторыми пунктами исследования функции:
1)Областью определения этой функции является множество всех действительных чисел. Эта функция не является четной или нечетной. График этой функции не имеет асимптот.
1) Найдем первую производную и определим соответствующие свойства
функции. f’(x)=3x2 – 6x –45. Решим уравнение 3х2 – 6х – 45 = 0. Корнями уравнения являются числа (-3) и 5.
Воспользуемся таблицей:
| х | (-¥; -3) | -3 | (-3;5) | (5;¥) | |
| f’(x) | + | - | + | ||
| f(x) | max | min |
Функция возрастает в интервалах (-¥;-3) и (5;¥), убывает в интервале (-3; 5).
Функция имеет максимальное значение f(-3)=101, имеет минимальное значение f(5)= - 155.
2) Найдем вторую производную f”(x)=(3x2 – 6x –45)’=6x-6.
Решим уравнение 6х-6=0. Решением уравнения является х=1.
Для определения свойств функции воспользуемся таблицей:
| х | (-¥; 1) | (1;¥) | |
| f”(x) | - | + | |
| f(x) | Ç выпуклая | точка перегиба | È вогнутая |
3) Для построения графика функции воспользуемся результатами вычислений, оформленными в виде таблицы:
| х | - 6 | -5 | -3 | - 1 | |||||||
| f(x) | - 34 | - 27 | -74 | -144 | -155 | -99 | |||||
| max | пер. | min |

1. Найти неопределенный интеграл:
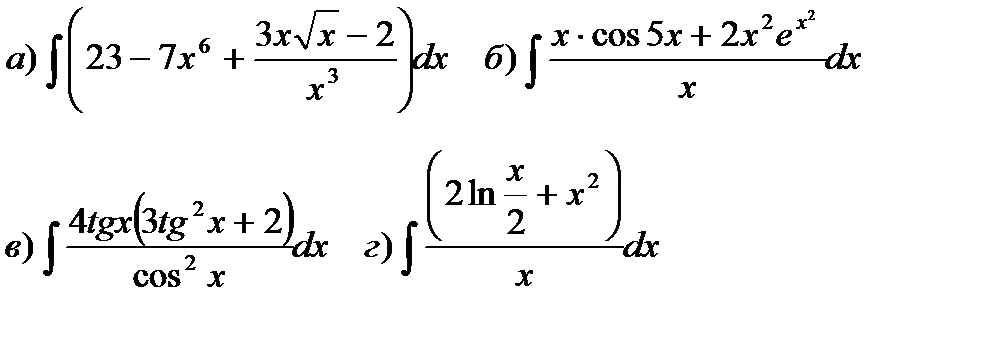
Решение:
При решении примеров следует пользоваться свойствами неопределенных интегралов, таблицей интегралов, в которую включена формула интеграла функции линейного аргумента, непосредственным интегрированием и методом подстановки.
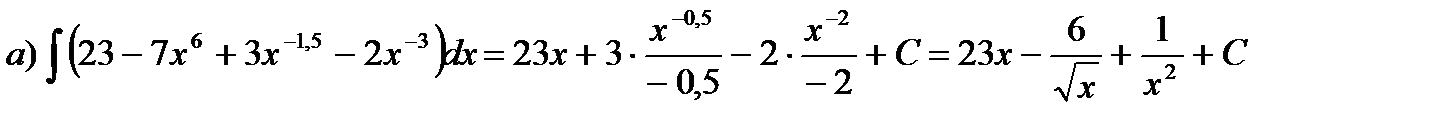
б) Выполнив почленное деление в подынтегральной функции, получим:
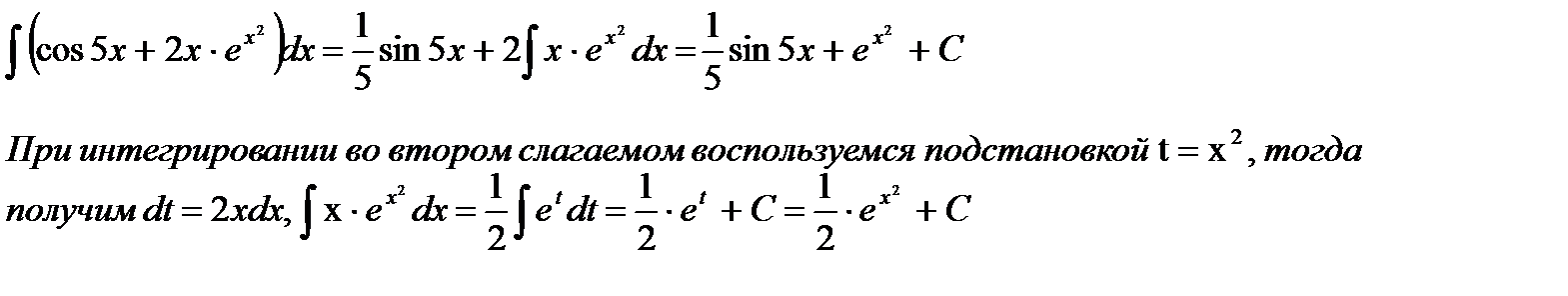
в)
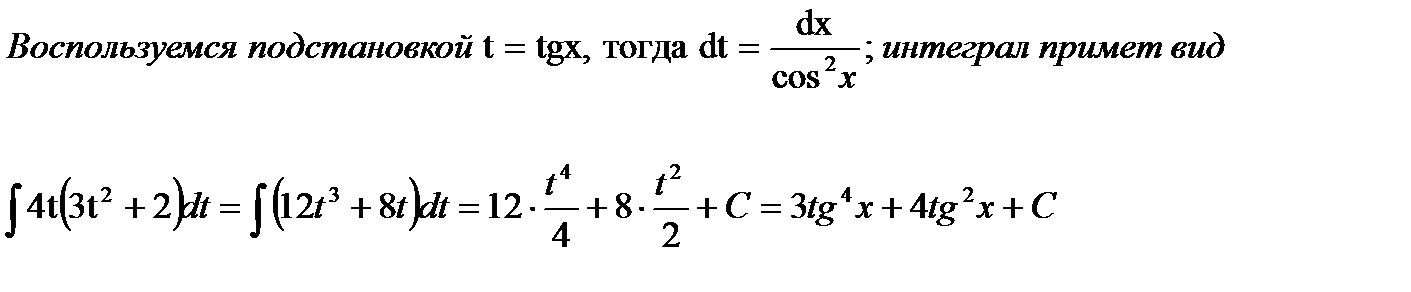
г) Будем использовать подстановку:
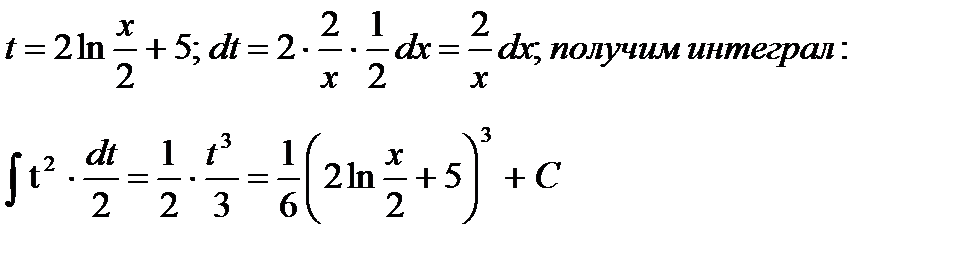
1. Вычислить определенный интеграл:
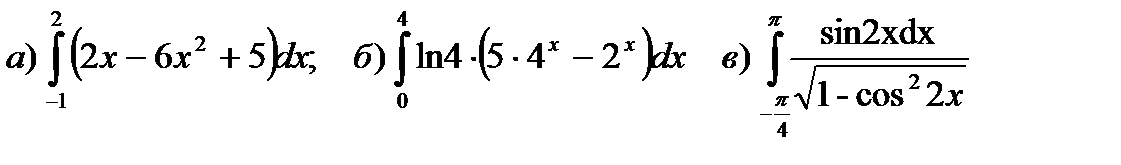
Решение:
При вычислении определенных интегралов используем формулу Ньютона-Лейбница
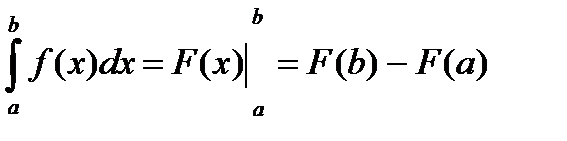 . Получение первообразной функции F(x) будем выполнять или непосредственно или способом подстановки.
. Получение первообразной функции F(x) будем выполнять или непосредственно или способом подстановки.
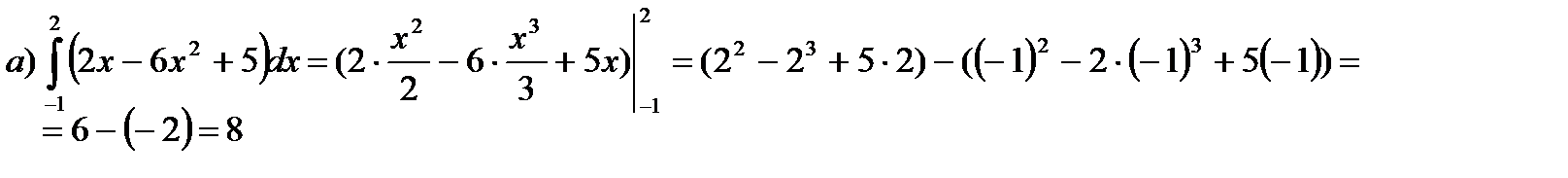
б)
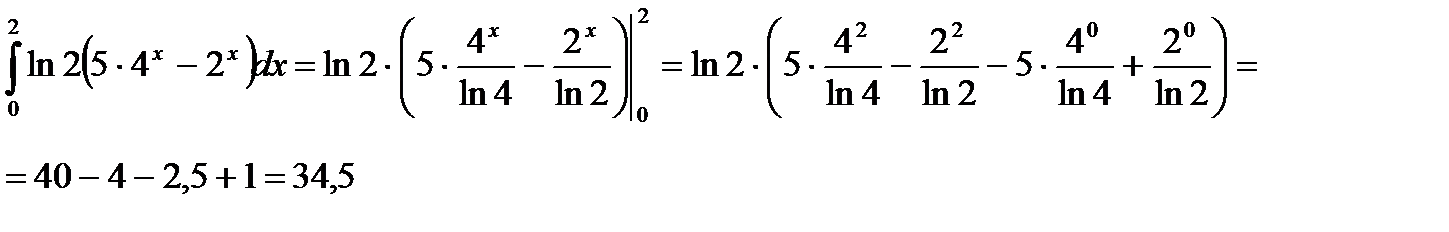

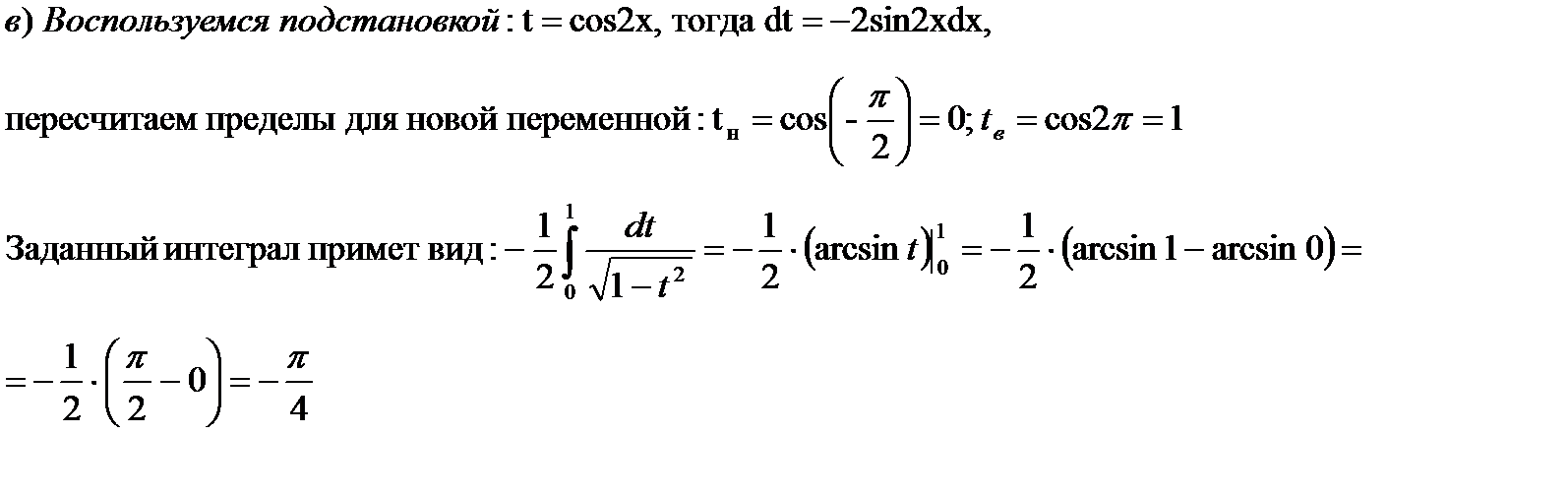
 2015-10-22
2015-10-22 782
782








