1. Найти общее решение (общий интеграл) дифференциального уравнения I порядка  .
.
Решение:
Правая часть уравнения  обладает свойством
обладает свойством  . Поэтому заданное уравнение является однородным дифференциальным уравнением I порядка. Совершим замену
. Поэтому заданное уравнение является однородным дифференциальным уравнением I порядка. Совершим замену  , где
, где  - некоторая функция от аргумента х. Отсюда
- некоторая функция от аргумента х. Отсюда  . Исходное уравнение приобретает вид
. Исходное уравнение приобретает вид  .
.
Продолжаем преобразования:  ;
;  .
.
Производим разделение переменных:  .
.
После интегрирования обеих частей уравнения получаем
 ;
;
 .
.
Таким образом  ;
;  .
.
Потенцируя, находим  или
или  ;
;  .
.
Итак, общий интеграл исходного уравнения приобретает вид
 , где С – произвольная постоянная.
, где С – произвольная постоянная.
2. Найти частное решение линейного однородного дифференциального уравнения II порядка с постоянными коэффициентами:
а) 
б) 
в) 
Решение:
а) Для заданного дифференциального уравнения  составим соответствующее характеристическое уравнение
составим соответствующее характеристическое уравнение  по принципу:
по принципу:  . Решаем полученное квадратное уравнение и получаем два вещественных разных корня
. Решаем полученное квадратное уравнение и получаем два вещественных разных корня  .
.
Т.к.  , то общее решение данных уравнений записывается в виде
, то общее решение данных уравнений записывается в виде  . В нашем случае
. В нашем случае  , где
, где  - произвольные постоянные.
- произвольные постоянные.
Отсюда  ,
,  .
.
Используя начальные условия  :
:  , т.е.
, т.е.  .
.
Из того что  следует
следует  , т.е.
, т.е.  ,
,  .
.
Решая систему уравнений  , получаем
, получаем  .
.
Теперь в наше общее решение  подставим найденные значения
подставим найденные значения  . Частное решение исходного уравнения, удовлетворяющее заданным начальным условиям, приобретает вид
. Частное решение исходного уравнения, удовлетворяющее заданным начальным условиям, приобретает вид  .
.
б) Для заданного дифференциального уравнения  составим соответствующее характеристическое уравнение
составим соответствующее характеристическое уравнение  по принципу:
по принципу:  . Решаем полученное квадратное уравнение и получаем два равных вещественных корня
. Решаем полученное квадратное уравнение и получаем два равных вещественных корня  .
.
Т.к.  , то общее решение данных уравнений записывается в виде
, то общее решение данных уравнений записывается в виде  . В нашем случае
. В нашем случае  , где
, где  - произвольные постоянные.
- произвольные постоянные.
Отсюда  ,
,  .
.
Учитывая начальные условия, получаем систему уравнений для определения  :
:  . Решая систему, получаем
. Решая систему, получаем  .
.
Искомое частное решение имеет вид: 
в) Для заданного дифференциального уравнения  составим соответствующее характеристическое уравнение
составим соответствующее характеристическое уравнение  . Решая это уравнение, убеждаем, что оно не имеет вещественных корней.
. Решая это уравнение, убеждаем, что оно не имеет вещественных корней.
В этом случае общее решение соответствующего дифференциального уравнения записывается в виде  , где
, где  - коэффициенты характеристического уравнения).
- коэффициенты характеристического уравнения).
У нас  поэтому общее решение заданного дифференциального уравнения имеет вид
поэтому общее решение заданного дифференциального уравнения имеет вид  .
.
Отсюда 
 .
.
Таким образом, для определения значений  исходя из начальных условий, получаем систему уравнений
исходя из начальных условий, получаем систему уравнений  ,
,
решая которую имеем  .
.
Итак, искомое частное решение приобретает вид

Комплексные числа
1. Построить на координатной плоскости числа Z1, Z2, где Z1=3-2i, Z2=-1+i.
Решение
На координатной плоскости изобразим точки (3; -2), (-1; 1) и соединим их с началом
координат, получив векторы, конечными точками которых являются заданные точки.
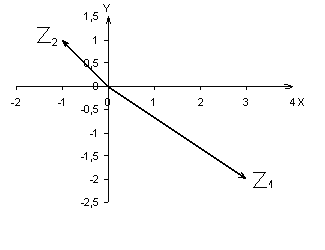
 2015-10-22
2015-10-22 2337
2337
