Высшая математика
Часть 4
Контрольные задания
Красноярск – 2001
Варианты контрольных заданий
В таблицах 1-2 приведены номера задач, входящих в контрольные работы: № 9 - «Интегральное исчисление функции многих переменной», № 10 - «Ряды». Студент должен выполнять контрольную работу по варианту, номер которого совпадает с последней цифрой номера его зачетной книжки. Первая цифра номера задачи соответствует номеру контрольной работы, а последняя - номеру варианта.
Таблица 1
Контрольная работа № 9
| Вариант | Номер задачи | |||||
| 9.1 | 9.11 | 9.21 | 9.31 | 9.41 | 9.51 | |
| 9.2 | 9.12 | 9.22 | 9.32 | 9.42 | 9.52 | |
| 9.3 | 9.13 | 9.23 | 9.33 | 9.43 | 9.53 | |
| 9.4 | 9.14 | 9.24 | 9.34 | 9.44 | 9.54 | |
| 9.5 | 9.15 | 9.25 | 9.35 | 9.45 | 9.55 | |
| 9.6 | 9.16 | 9.26 | 9.36 | 9.46 | 9.56 | |
| 9.7 | 9.17 | 9.27 | 9.37 | 9.47 | 9.57 | |
| 9.8 | 9.18 | 9.28 | 9.38 | 9.48 | 9.58 | |
| 9.9 | 9.19 | 9.29 | 9.39 | 9.49 | 9.59 | |
| 9.10 | 9.20 | 9.30 | 9.40 | 9.50 | 9.60 |
Таблица 2
Контрольная работа № 10
| Вариант | Номер задачи | ||||
| 10.1 | 10.1 | 10.21 | 10.31 | 10.41 | |
| 10.2 | 10.12 | 10.22 | 10.32 | 10.42 | |
| 10.3 | 10.13 | 10.23 | 10.33 | 10.43 | |
| 10.4 | 10.14 | 10.24 | 10.34 | 10.44 | |
| 10.5 | 10.15 | 10.25 | 10.35 | 10.45 | |
| 10.6 | 10.16 | 10.26 | 10.36 | 10.46 | |
| 10.7 | 10.17 | 10.27 | 10.37 | 10.47 | |
| 10.8 | 10.18 | 10.28 | 10.38 | 10.48 | |
| 10.9 | 10.19 | 10.29 | 10.39 | 10.49 | |
| 10.10 | 10.20 | 10.30 | 10.40 | 10.50 |
Условия заданий контрольных работ
Интегральное исчисление функции многих переменной (к. р. № 9)
9.1 - 9.10. Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной данными линиями, заданными уравнениями в декартовых координатах. Сделать чертеж данной фигуры.
9.1. 
9.2. 
9.3. 
9.4. 
9.5. 
9.6. 
9.7. 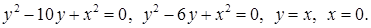
9.8. 
9.9. 
9.10. 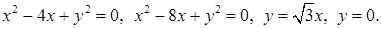
9.11 - 9.20. Вычислить при помощи тройного интеграла в цилиндрических координатах объем тела, ограниченного указанными поверхностями. Сделать чертеж.
9.11. 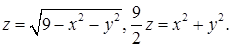
9.12. 
9.13. 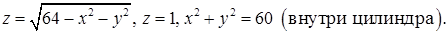
9.14. 
9.15. 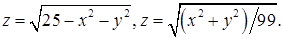
9.16. 
9.17. 
9.18. 
9.19. 
9.20. 
9.21 – 9.30. Вычислить криволинейный интеграл I-го рода.
9.21.  ,
,  – отрезок прямой
– отрезок прямой  , заключенный между точками
, заключенный между точками 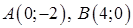 .
.
9.22.  ,
,  – отрезок прямой
– отрезок прямой  , заключенный между точками
, заключенный между точками 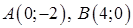 .
.
9.23.  ,
,  – отрезок прямой, соединяющей точки
– отрезок прямой, соединяющей точки 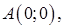
 .
.
9.24.  ,
,  – первый виток винтовой линии
– первый виток винтовой линии 
 .
.
9.25.  ,
,  – окружность
– окружность 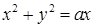 .
.
9.26.  ,
,  – первый виток конической винтовой линии
– первый виток конической винтовой линии  .
.
9.27. 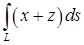 ,
,  – дуга кривой
– дуга кривой  .
.
9.28.  ,
,  – первая арка циклоиды
– первая арка циклоиды 
 .
.
9.29. 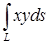 , где
, где  – четверть эллипса
– четверть эллипса  , лежащая в первом квадранте.
, лежащая в первом квадранте.
9.30. 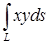 , где
, где  – контур квадрата
– контур квадрата  .
.
9.31 – 9.40. Даны векторное поле  и плоскость P:
и плоскость P:  , которая совместно с координатными плоскостями образует пирамиду V. Пусть
, которая совместно с координатными плоскостями образует пирамиду V. Пусть 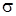 – основание пирамиды, принадлежащее плоскости P;
– основание пирамиды, принадлежащее плоскости P;  – нормаль к
– нормаль к 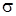 , направленная вне пирамиды V. Требуется вычислить
, направленная вне пирамиды V. Требуется вычислить
1) поток векторного поля  через поверхность
через поверхность 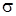 в направлении
в направлении  ;
;
2) поток векторного поля  через полную поверхность пирамиды V в направлении внешней нормали к её поверхности, непосредственно и применив теорему Гаусса-Остроградского.
через полную поверхность пирамиды V в направлении внешней нормали к её поверхности, непосредственно и применив теорему Гаусса-Остроградского.
3) Сделать чертеж.
9.31. 
9.32. 
9.33. 
9.34. 
9.35. 
9.36. 
9.37. 
9.38. 
9.39. 
9.40. 
9.41 – 9.50. Даны векторное поле  и контур
и контур  . Вычислить циркуляцию вектора
. Вычислить циркуляцию вектора  по контуру
по контуру  непосредственно и пользуясь формулой Стокса.
непосредственно и пользуясь формулой Стокса.
9.41. 
9.42. 
9.43. 
9.44. 
9.45. 
9.46. 
9.47. 
9.48. 
9.49. 
9.50. 
9.51. – 9.60. Дано векторное поле  . Проверить, будет ли потенциальным и соленоидальным поле
. Проверить, будет ли потенциальным и соленоидальным поле  . В случае потенциальности поля найти его потенциал
. В случае потенциальности поля найти его потенциал  .
.
9.51. 
9.52. 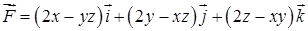
9.53. 
9.54. 
9.55. 
9.56. 
9.57. 
9.58. 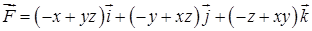
9.59. 
9.60. 
Ряды (к. р. № 10)
10.1 – 10.10. Исследовать сходимость числового ряда.
10.1.  ;
;  .
.
10.2.  ;
;  .
.
10.3.  ;
;  .
.
10.4.  ;
;  .
.
10.5.  ;
;  .
.
10.6. 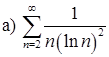 ;
;  .
.
10.7.  ;
;  .
.
10.8.  ;
;  .
.
10.9.  ;
;  .
.
10.10.  ;
;  .
.
10.11. – 10.20. Исследовать на абсолютную и условную сходимость знакочередующийся ряд.
10.11.  . 10.12.
. 10.12.  .
.
10.13.  . 10.14.
. 10.14.  .
.
10.15.  . 10.16.
. 10.16.  .
.
10.17. 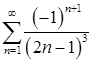 . 10.18.
. 10.18.  .
.
10.19. 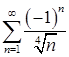 . 10.20.
. 10.20.  .
.
10.21 – 10.30. Найти интервал сходимости степенного ряда и исследовать его сходимость на концах интервала.
10.21.  . 10.22.
. 10.22.  .
.
10.23.  . 10.24.
. 10.24.  .
.
10.25.  . 10.26.
. 10.26.  .
.
10.27.  . 10.28.
. 10.28.  .
.
10.29. 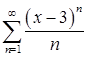 . 10.30.
. 10.30.  .
.
10.31 – 10.40. Вычислить определенный интеграл  с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.
с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.
10.31.  . 10.32.
. 10.32.  .
.
10.33.  . 10.34.
. 10.34.  .
.
10.35.  . 10.36.
. 10.36.  .
.
10.37.  . 10.38.
. 10.38.  .
.
10.39.  . 10.40.
. 10.40.  .
.
10.41. – 10.50. Найти три первых, отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения, удовлетворяющего заданным начальным условиям.
10.41.  .
.
10.42.  .
.
10.43. 
10.44.  .
.
10.45.  .
.
10.46. 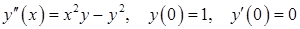 .
.
10.47.  .
.
10.48.  .
.
10.49.  .
.
10.50.  .
.
СПИСОК ЛИТЕРАТУРЫ
1. Пискунов Н. С. Дифференциальное и интегральное исчисления. Т. 2. М.: Наука, 1985.
2. Бугров Я. С., Никольский С. М. Дифференциальное и интегральное исчисление. М.: Наука, 1984.
3. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. М.: Наука, 1981.
4. Щипачев В. С. Основы высшей математики. М.: Высш. шк., 1989.
5. Данко П.Е., Попов А.Г., Кожевников Т.Я. Высшая математика в упражнениях и задачах. Т. 2. М.: Высшая школа, 1986.
 2015-10-22
2015-10-22 363
363







