Высшая математика
Красноярск - 2001
Варианты контрольных заданий
В таблицах 1–3 приведены номера задач, входящих в задания контрольной работы № 1 “Элементы линейной и векторной алгебры”, контрольной работы № 2 “Аналитическая геометрия” и контрольной работы № 3 “Введение в математический анализ”. Студент должен выполнять контрольную работу по варианту, номер которого совпадает с последней цифрой его зачетной книжки.
Таблица 1
Контрольная работа № 1
| Вариант | Номера задач контрольной работы № 1 | |||||
Таблица 2
Контрольная работа № 2
| Вариант | Номера задач контрольной работы № 2 | ||||||
Таблица 3
Контрольная работа № 3
| Вариант | Номера задач контрольной работы № 3 | ||||
Условия заданий контрольных работ
I. Элементы линейной и векторной алгебры (к. р. №1).
1–10. Вычислить определитель четвертого порядка.
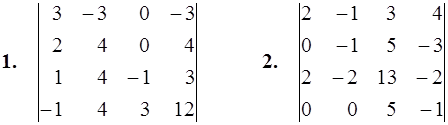
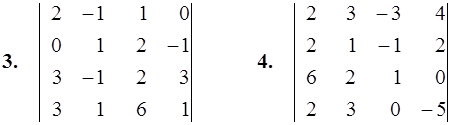
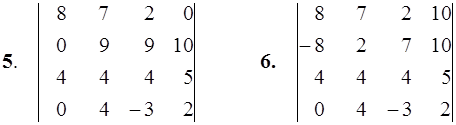
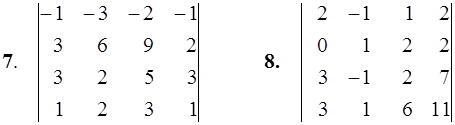
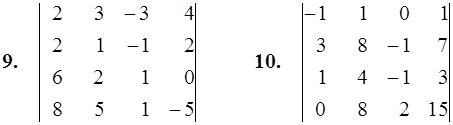
11–20. Дана система линейных уравнений. Доказать ее совместность и решить двумя способами: 1) по формулам Крамера; 2) матричным методом.
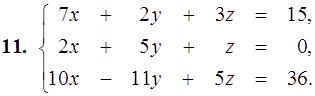
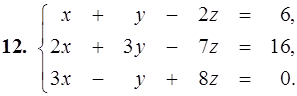
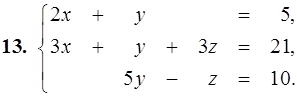
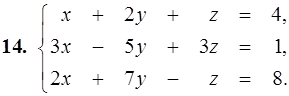
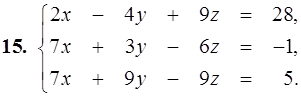
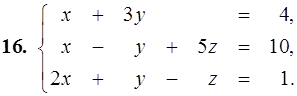
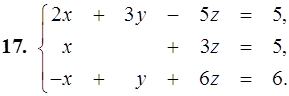
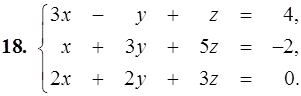
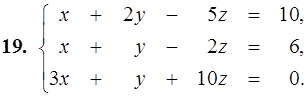
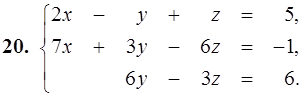
21–30. Записать систему линейных уравнений по ее расширенной матрице G. Исследовать совместность полученной системы и решить ее методом Гаусса.
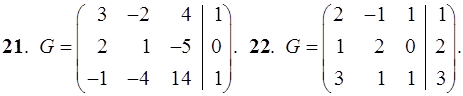
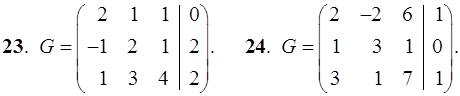
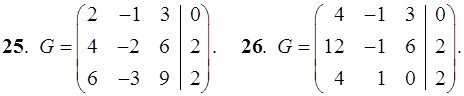
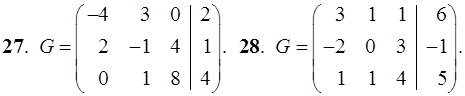
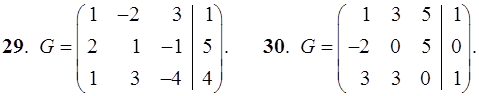
31–40. Даны координаты вершин пирамиды ABCD. Найти: 1) угол между ребрами AB и AC; 2) площадь и высоту BF треугольника BCD; 3) объем пирамиды ABCD и высоту, опущенную из точки A на грань BCD.
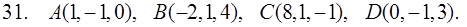
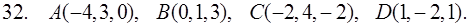
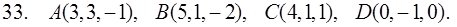
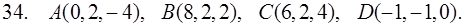
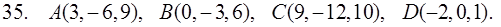
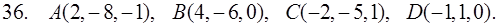
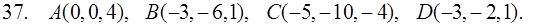
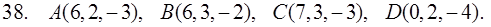
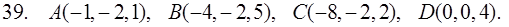
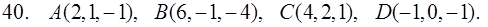
41–50. Даны векторы 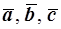 в некотором базисе. Найти:
в некотором базисе. Найти:
1) проекцию вектора 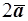 на вектор
на вектор 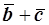 ;
;
Проверить, образуют ли векторы 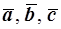 базис? Если да, то какой базис: левый или правый?
базис? Если да, то какой базис: левый или правый?
41. 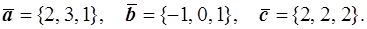
42. 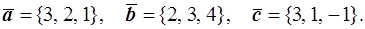
43. 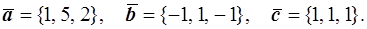
44. 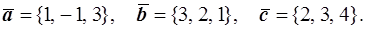
45. 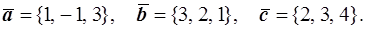
46. 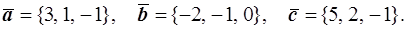
47. 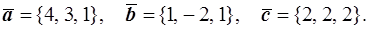
48. 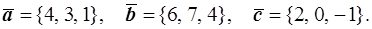
49. 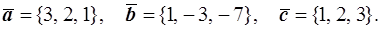
50. 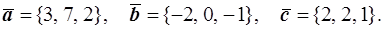
51–60. Пусть 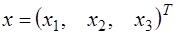 – координаты произвольного вектора линейного пространства, заданные в некотором базисе. Известен закон изменения координат вектора под действием преобразования
– координаты произвольного вектора линейного пространства, заданные в некотором базисе. Известен закон изменения координат вектора под действием преобразования 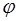 .
.
1. Доказать, что 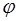 – линейное преобразование.
– линейное преобразование.
2. Составить матрицу линейного преобразования 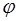 в том же базисе, в котором заданы координаты вектора
в том же базисе, в котором заданы координаты вектора 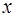 .
.
3. Найти образ вектора 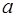 и прообраз вектора
и прообраз вектора 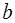 под действием преобразования
под действием преобразования 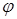 .
.
4. Найти собственные векторы и собственные значения преобразования 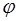 .
.
51. 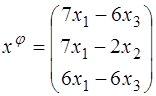 ;
; 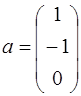 ;
; 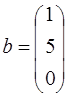 .
.
52. 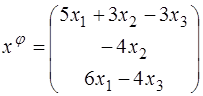 ;
; 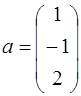 ;
; 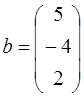 .
.
53. 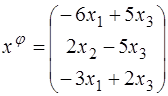 ;
; 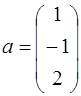 ;
; 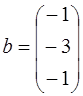 .
.
54. 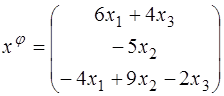 ;
; 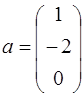 ;
; 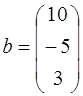 .
.
55. 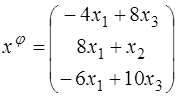 ;
; 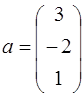 ;
; 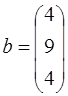 .
.
56. 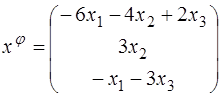 ;
; 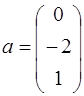 ;
; 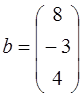 .
.
57. 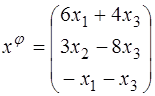 ;
; 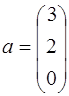 ;
; 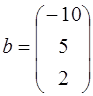 .
.
58. 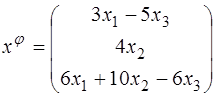 ;
; 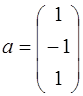 ;
; 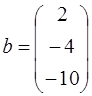 .
.
59. 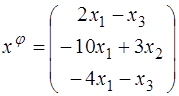 ;
; 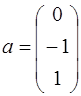 ;
; 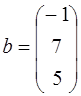 .
.
60. 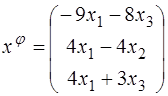 ;
; 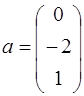 ;
; 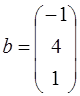 .
.
II. Элементы аналитической геометрии (к.р. №2)
61. Уравнение одной из сторон квадрата x+3y–5=0. Составить уравнения трех остальных сторон квадрата, если P(–1;0) – точка пересечения его диагоналей. Сделать чертеж.
62. Даны уравнения одной из сторон ромба x–3y+10=0 и одной из его диагоналей x+4y–4=0; диагонали ромба пересекаются в точке P(0;1). Найти уравнения остальных сторон ромба. Сделать чертеж.
63. Уравнения двух сторон параллелограмма x+2y+2=0 и x+y–4=0, а уравнение одной из его диагоналей x–2=0. Найти координаты вершин параллелограмма. Сделать чертеж.
64. Даны две вершины A(–3; 3) и B(5;–1) и точка D(4; 3) пересечения высот треугольника. Составить уравнения его сторон. Сделать чертеж.
65. Даны вершины A(–3,–2), B(4;–1), C(1; 3) трапеции ABCD (AD||BC). Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины D этой трапеции. Сделать чертеж.
66. Даны уравнения двух сторон треугольника 5x–4y+15=0 и 4x+y–9=0. Его медианы пересекаются в точке P(0; 2). Составить уравнение третьей стороны треугольника. Сделать чертеж.
67. Даны вершины A(2,–2), B(3; –1), P(1; 0) пересечения медиан треугольника ABC. Составить уравнение высоты треугольника, проведенной через третью вершину С. Сделать чертеж.
68. Даны уравнения двух высот треугольника x+y=4 и y=2x и одна из его вершин A(0; 2). Составить уравнения сторон треугольника. Сделать чертеж.
69. Даны уравнения двух медиан треугольника x–2y+1=0 и y–1=0 и одна из его вершин A(1; 3). Составить уравнения сторон треугольника. Сделать чертеж.
70. Две стороны треугольника заданы уравнениями 5x–2y–8=0 и 3x–2y–8=0, а середина третьей стороны совпадает с началом координат. Составить уравнение этой стороны. Сделать чертеж.
71. Составить уравнение и построить линию, расстояние каждой точки которой от начала координат и от точки А(5; 0) относятся как 2:1.
72. Составить уравнение и построить линию, расстояние каждой точки которой от точки А(–1; 0) вдвое меньше расстояния ее от прямой x=–4.
73. Составить уравнение и построить линию, расстояние каждой точки которой от точки А(2; 0) и от прямой 5x+8=0 относятся как 5: 4.
74. Составить уравнение и построить линию, каждая точка которой находится вдвое дальше от точки А(4; 0), чем от точки B(1;0).
75. Составить уравнение и построить линию, расстояние каждой точки которой от точки А(2; 0)и от прямой 2x+5=0 относятся как 4: 5.
76. Составить уравнение и построить линию, расстояние каждой точки которой от точки А(3; 0) вдвое меньше расстояния от точки B(26;0).
77. Составить уравнение и построить линию, каждая точка которой одинаково удалена от точки А(0; 2) и от прямой y–4=0.
78. Составить уравнение и построить линию, расстояние каждой точки которой от начала координат и от точки А(3; 0)относятся как 1: 2.
79. Составить уравнение и построить линию, каждая точка которой равноудалена от точки А(2; 6) и от прямой y+2=0.
80. Составить уравнение и построить линию, каждая точка которой отстоит от точки А(–4; 0) втрое дальше, чем от начала координат.
81–90. Привести заданное уравнение линии второго порядка к каноническому виду и построить ее.
81. 2x2–y2+x+2y=0.
82. x2+y2=2x+4y.
83. 2x2+3y2–4x+6x=0.
84. x2+4y2+1=2y.
85. 2x2+y2+6y=0.
86. 2x–x2+2y2=0.
87. 2x2–y2+4y=0.
88. x+2y–y2=0.
89. 2x2+x+2y2–4y=0.
90. x2+2x+4y2=2.
91–100. Даны уравнение плоскости P Ax+By+Cz+D=0,
канонические уравнения прямой L
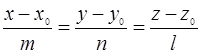
и координаты двух точек E и F. Найти: 1) уравнение плоскости, проходящей через точку E параллельно плоскости P; 2) уравнение плоскости, проходящей через точку F перпендикулярно прямой L; 3) угол между плоскостью P и прямой L; 4) расстояние от точки E до плоскости P; 5) уравнение плоскости, проходящей через начало координат и точки E и F.
91. P: 5x–y+2z+1=0; E(1,–1, 2), F(1, 3, 3);
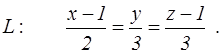
92. P: 2x+2y+z–5=0; E(–1,0, 3), F(0, 2, 2);
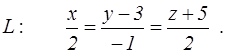
93. P: x+5y–z+7=0; E(2, 1, 3), F(0, –1, 2);
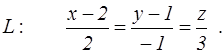
94. P: 2x+y–z+6=0; E(2, 3, 4), F(–1, 0, 1);
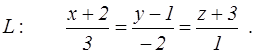
95. P: 3x+y–5z+4=0; E(1, –3, 2), F(2, 4, 1);
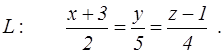
96. P: 2x+5y–4z=0; E(1, 1, 1), F(–1, 0, 3);
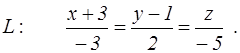
97. P: 3x+y–5z–1=0; E(1, 2, –4), F(3, 1, 1);
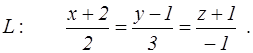
98. P: 6x–5y+8z+1=0; E(1, 0, 1), F(–1, 3, 2);
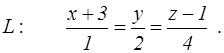
99. P: 6x–y+z+3=0; E(–1, 0, –1), F(2, 1, 3);
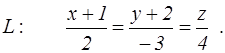
100. P: 6x+8z–4=0; E(–1, 3, 0), F(2, 1, 2);
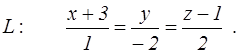
101–110. Построить тело, ограниченное заданными поверхностями.
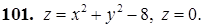
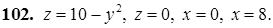
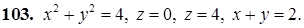
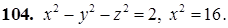
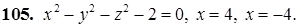
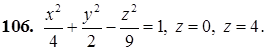
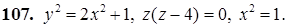
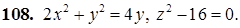
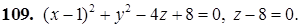
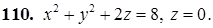
111–120. Линия задана уравнением r=r(j) в полярной системе координат. Требуется: построить линию по точкам начиная от j=0 до j=2p, придавая значения с шагом p/8; найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью.
111. 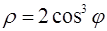 . 112.
. 112. 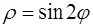 .
.
113. 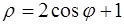 . 114.
. 114. 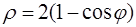 .
.
115. 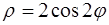 . 116.
. 116. 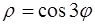 .
.
117. 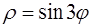 . 118.
. 118. 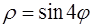 .
.
119. 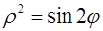 . 120.
. 120. 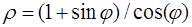 .
.
121–130. Выполнить следующие задания.
1. Решить уравнение 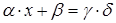 .
.
2. Найти значение выражения 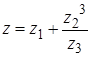 .
.
3. Найти и изобразить на комплексной плоскости корни уравнения 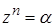 .
.
121. 1. 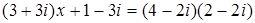 .
.
2. 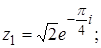
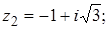
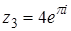 .
.
3. 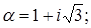
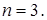
122. 1. 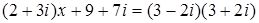 .
.
2. 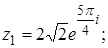
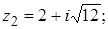
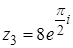 .
.
3. 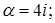
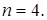
123. 1. 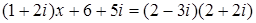 .
.
2. 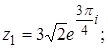
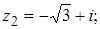
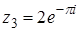 .
.
3. 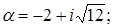
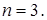
124. 1. 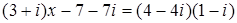 .
.
2. 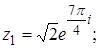
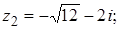
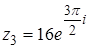 .
.
3. 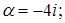
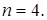
125. 1. 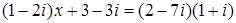 .
.
2. 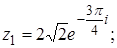
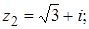
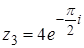 .
.
3. 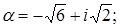
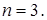
126. 1. 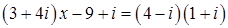 .
.
2. 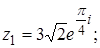
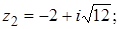
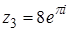 .
.
3. 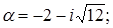
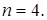
127. 1. 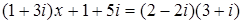 .
.
2. 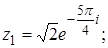
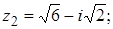
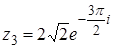 .
.
3. 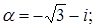
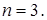
128. 1. 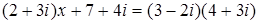 .
.
2. 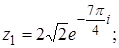
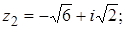
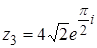 .
.
3. 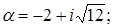
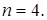
129. 1. 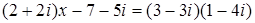 .
.
2. 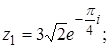
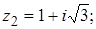
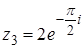 .
.
3. 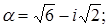
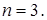
130. 1. 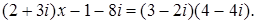
2. 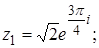
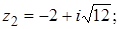
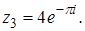
3. 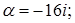
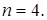
III. Введение в математический анализ (к. р. №3)
131–140. Найти область определения функции.
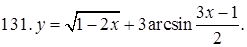
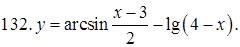
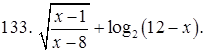
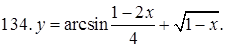
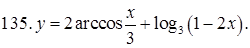
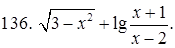
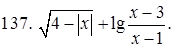
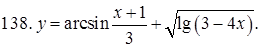
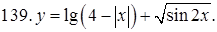
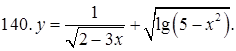
141–150. Построить график функции, используя преобразование одной из элементарных функций: 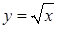 ,
, 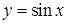 ,
, 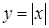 ,
, 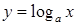 .
.
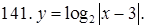
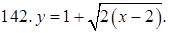
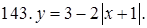
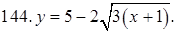
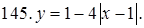
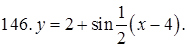
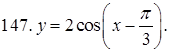
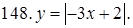
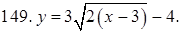
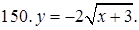
151–160. Найти пределы функций, не пользуясь правилом Лопиталя.
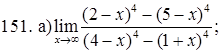
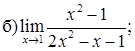
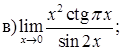
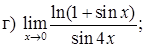
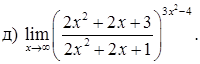
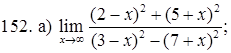
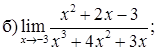
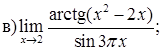
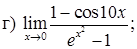
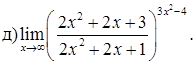
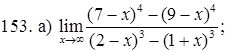
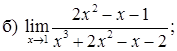
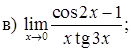
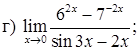
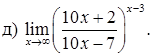
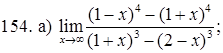
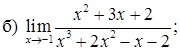
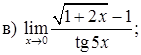
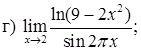
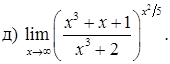
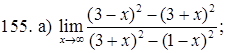
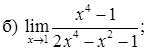
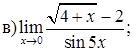
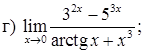
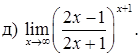
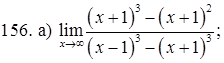
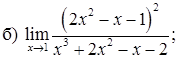
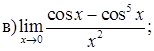
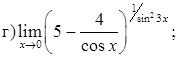
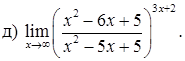
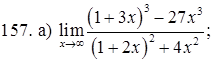
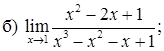
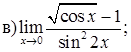
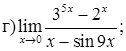
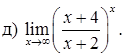
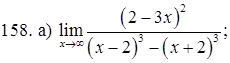
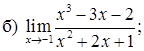
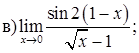
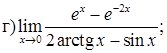
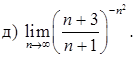
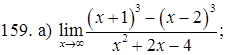
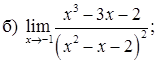
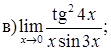
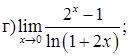
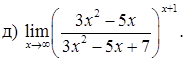
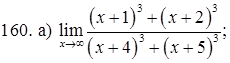
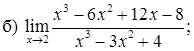
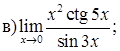
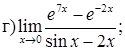
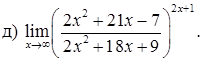
161–170. Найти точки разрыва функций, исследовать их характер:
а) построить графики функций (схематично);
б) исследовать на непрерывность функцию на соответствующих отрезках.
161. а) 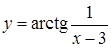 ;
;
б) 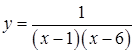 на отрезках
на отрезках  ,
, 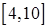 ,
, 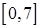 .
.
162. а) 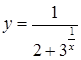 ;
;
б) 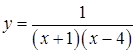 на отрезках
на отрезках 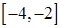 ,
, 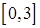 ,
, 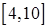 .
.
163. а) 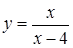 ;
;
б) 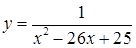 на отрезках
на отрезках 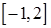 ,
, 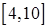 ,
, 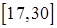 .
.
164. а) 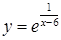 ;
;
б) 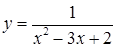 на отрезках
на отрезках 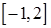 ,
, 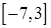 ,
, 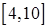 .
.
165. а) 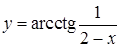 ;
;
б) 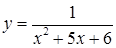 на отрезках
на отрезках 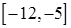 ,
, 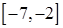 ,
, 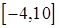 .
.
166. а) 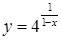 ;
;
б) 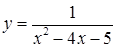 на отрезках
на отрезках 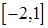 ,
, 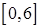 ,
, 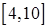 .
.
167. а) 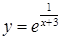 ;
;
б) 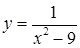 на отрезках
на отрезках 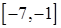 ,
, 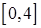 ,
, 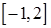 .
.
168. а) 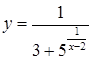 ;
;
б) 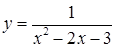 на отрезках
на отрезках 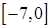 ,
, 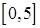 ,
, 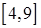 .
.
169. а) 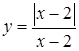 ;
;
б) 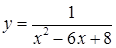 на отрезках
на отрезках 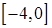 ,
, 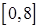 ,
, 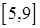 .
.
170. а) 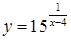 ;
;
б) 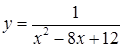 на отрезках
на отрезках 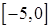 ,
, 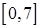 ,
, 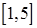 .
.
171–180. Задана функция 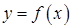 . Найти точки разрыва функции, если они существуют, исследовать их характер. Сделать чертеж.
. Найти точки разрыва функции, если они существуют, исследовать их характер. Сделать чертеж.
171. 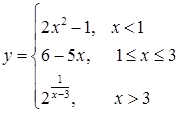 172.
172. 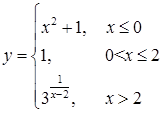
173. 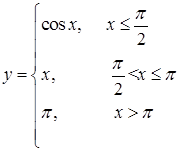 174.
174. 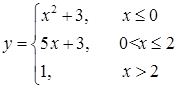
175. 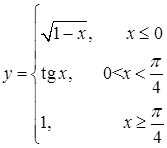 176.
176. 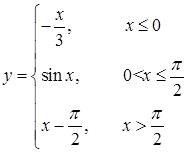
177. 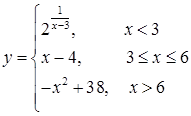 178.
178. 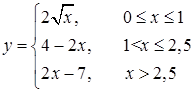
179. 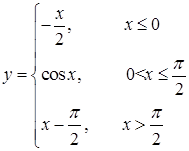 180.
180. 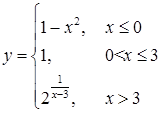
СПИСОК ЛИТЕРАТУРЫ
1. Пискунов Н. С. Дифференциальное и интегральное исчисления. Т. 2. М.: Наука, 1985.
2. Бугров Я. С., Никольский С. М. Дифференциальное и интегральное исчисление. М.: Наука, 1984.
3. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. М.: Наука, 1981.
4. Щипачев В. С. Основы высшей математики. М.: Высш. шк., 1989.
5. Данко П.Е., Попов А.Г., Кожевников Т.Я. Высшая математика в упражнениях и задачах. Т. 2. М.: Высш. шк., 1986.
 2015-10-22
2015-10-22 1004
1004

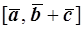 .
.






