Для функций нескольких переменных могут быть введены понятия предела и непрерывности. Введенные ранее понятия предела и непрерывности для функции одной переменной представляют собой частный случай этих понятий для функций нескольких перменных.
Число А называется пределом функции y = f(X) = f(х1, х2, …хn) при Х, стремящемся к Х(0) = (х1(0), х2(0), …хn(0)) (или в точке Х(0)), если для любого, даже сколь угодно малого положительного числа e, найдется такое положительное число d (зависящее от e, т.е. d = d (e)), что для всех точек Х, отстоящих от Х(0)на расстояние, меньшее d, (кроме, разве что, самой точки Х(0), т.е. при  ) верно неравенство: |f(Х) - А| < e.
) верно неравенство: |f(Х) - А| < e.
Предел функции в точке Х(0)обозначается  или
или
f(X) ® А при X ® Х(0)или  .
.
Итак, число А есть предел функции у = f(X) при X ® Х(0), если для любого e > 0 найдется такая d-окрестность точки Х(0), что для всех точек из этой окрестности значения функции f(Х) будут заключены в e-окрестности точки А на числовой оси значений функции.
Вычисление пределов функций многих переменных значительно сложнее, чем в случае функций одной переменной. Если на прямой существуют всего два направления, по которым аргумент может стремиться к предельной точке (справа и слева), то в простанствах большей размерности (даже в двумерном пространстве - на плоскости) таких направлений бесконечное много, и пределы функции по разным направлениям могут не совпадать. Однако, в некоторых случаях такие пределы вычисляются достаточно легко (пример - см. учебник Кремера стр. 407).
Функция многих переменных называется непрерывной в точке, если она определена в этой точке, имеет в ней конечный предел, и этот предел равен значению функции в этой точке, т.е. 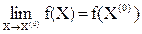 .
.
Геометрический смысл непрерывности функции двух переменных заключается в том, что график этой функции представляет собой сплошную поверхность.
 2015-10-22
2015-10-22 1362
1362
