Производная по направлению

Вводя понятие частной производной функции многих переменных, мы давали приращение переменным по отдельности, оставляя все остальные аргументы неизменными. В частности, если рассматривать функцию двух переменных z = f(x,y), то либо переменной x давалось приращение Δx, и тогда в области определения функции происходил переход из точки с координатами (x,y) в точку с координатами (x + Δx; y); либо переменной y давалось приращение Δy, и тогда в области определения функции происходил переход из точки с координатами (x,y) в точку с координатами (x; y + Δy) (см. рисунок 5.6). Таким образом, точка, в которой мы брали частную производную функции, перемещалась в направлениях, параллельных координатным осям на плоскости (либо параллельно оси абсцисс, либо параллельно оси ординат). Рассмотрим теперь случай, когда направление может быть взято произвольно, т.е. приращения даются сразу нескольким переменным. Для случая функции двух переменных мы перейдем в точку (x + Δx; y + Δy), при этом перемещение составит Δ l (см. рисунок 5.6).

При перемещении в данном направлении функция z получит приращение Δ _l z = f(x + Δx; y + Δy) – f(x,y), называемое приращением функции z в данном направлении l.

Производной z _l ` по направлению l функции двух переменных
z = f(x,y) называют предел отношения приращения функции в этом направлении к величине перемещения Δ l при стремлении последней к нулю, т.е. .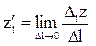

Производная z _l ` характеризует скорость изменения функции в направлении l.

Понятие производной по направлению может быть обобщено на функции с любым числом переменных.

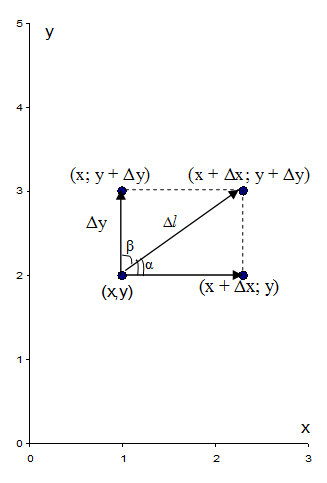
Рисунок 5.6 – Перемещение точки по направлению l

Можно доказать, что z _l ` = z<sub>х</sub>`cos α + z_у`cos β, где α и β – углы, образованные направлением перемещения точки с осями координат (см. рисунок 5.6).

Например, найдем производную функции z = ln (x² + xy) в точке
(3; 1) в направлении, идущем от этой точки к точке (6; -3) (см. рисунок 5.7).

Для этого вначале найдем частные производные этой функции в точке (3; 1): z_x` = (2x + y)/(x<sup>2</sup> + xy) = (2*3 + 1)/(3<sup>2</sup> + 3*1) = 7/12;
z<sub>y</sub>` = x/(x² + xy) = 3/(3² + 3*1) = 3/12 = 1/4.

Отметим, что Δx = 6 – 3 = 3; Δy = -3 – 1 = -4; (Δ l)² = 9 + 16 = 25;
|Δ l | = 5. Тогда cos α = 3/5; cos β = -4/5; z _l ` = z<sub>х</sub>`cos α + z_у`cos β = (7/12)*(3/5) - (1/4)*(4/5) = (7/4)*(1/5) - (1/4)*(4/5) = (7*1 – 1*4)/(4*5) = 3/20.

Рисунок 5.7 – Перемещение точки (3; 1) в направлении, идущем
к точке (6; -3)

Градиент функции

Из школьного курса математики известно, что вектор на плоскости представляет собой направленный отрезок. Его начало и конец имеют по две координаты. Координаты вектора рассчитываются путем вычитания из координат конца координат начала.

Понятие вектора может быть распространено и на n-мерное пространство (вместо двух координат будет n координат).

Градиентом grad z функции z = f(х₁, х₂, …х_n) называется вектор частных производных функции в точке, т.е. вектор с координатами .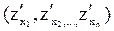

Можно доказать, что градиент функции характеризует направление наискорейшего роста уровня функции в точке.

Например, для функции z = 2х₁ + х₂ (см. рисунок 5.8) градиент в любой точке будет иметь координаты (2; 1). Построить его на плоскости можно различными способами, взяв в качестве начала вектора любую точку. Например, можно соединить точку (0; 0) с точкой (2; 1), или точку (1; 0) с точкой (3; 1), или точку (0; 3) с точкой (2; 4), или т.п. (см. рисунок 5.8). Все построенные таким образом вектора будут иметь координаты (2 – 0; 1 – 0) =
= (3 – 1; 1 – 0) = (2 – 0; 4 – 3) = (2; 1).

Из рисунка 5.8 хорошо видно, что уровень функции растет в направлении градиента, поскольку построенные линии уровня соответствуют значениям уровня 4 > 3 > 2.

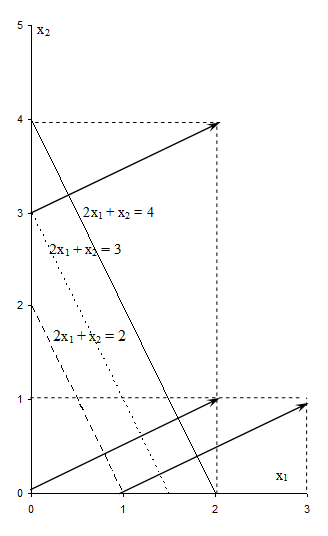
Рисунок 5.8 - Градиент функции z = 2х₁ + х₂

Рассмотрим другой пример – функцию z = 1/(х₁х₂). Градиент этой функции уже не будет всегда одинаковым в разных точках, поскольку его координаты определяются формулами (-1/(х₁²х₂); -1/(х₁х₂²)).

На рисунке 5.9 представлены линии уровня функции z = 1/(х₁х₂) для уровней 2 и 10 (прямая 1/(х₁х₂) = 2 обозначена пунктиром, а прямая
1/(х₁х₂) = 10 – сплошной линией).

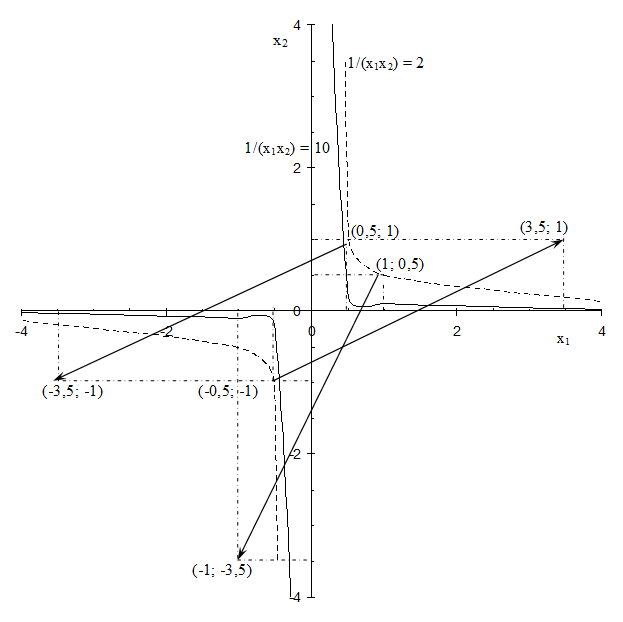
Рисунок 5.9 - Градиенты функции z = 1/(х₁х₂) в различных точках

Возьмем, например, точку (0,5; 1) и вычислим градиент в этой точке: (-1/(0,5²*1); -1/(0,5*1²)) = (-4; -2). Заметим, что точка (0,5; 1) лежит на линии уровня 1/(х₁х₂) = 2, ибо z = f(0,5; 1) = 1/(0,5*1) = 2. Чтобы изобразить вектор (-4; -2) на рисунке 5.9, соединим точку (0,5; 1) с точкой (-3,5; -1), ибо
(-3,5 – 0,5; -1 - 1) = (-4; -2).

Возьмем другую точку на той же самой линии уровня, например, точку (1; 0,5) (z = f(1; 0,5) = 1/(0,5*1) = 2). Вычислим градиент в этой точке
(-1/(1²*0,5); -1/(1*0,5²)) = (-2; -4). Чтобы изобразить его на рисунке 5.9, соединим точку (1; 0,5) с точкой (-1; -3,5), ибо (-1 - 1; -3,5 - 0,5) = (-2; -4).

Возьмем еще одну точку на той же самой линии уровня, но только теперь в неположительной координатной четверти. Например, точку (-0,5; -1) (z = f(-0,5; -1) = 1/((-1)*(-0,5)) = 2). Градиент в этой точке будет равен
(-1/((-0,5)²*(-1)); -1/((-0,5)*(-1)²)) = (4; 2). Изобразим его на рисунке 5.9, соединив точку (-0,5; -1) с точкой (3,5; 1), ибо (3,5 – (-0,5); 1 – (-1)) = (4; 2).

Следует обратить внимание, что во всех трех рассмотренных случаях градиент показывает направление роста уровня функции (в сторону линии уровня 1/(х₁х₂) = 10 > 2).

Можно доказать, что градиент всегда перпендикулярен линии уровня (поверхности уровня), проходящей через данную точку.