Уравнение вида 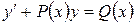 (III)
(III)
называют линейным дифференциальным уравнением. Если 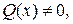 то уравнение называется линейным неоднородным, если
то уравнение называется линейным неоднородным, если 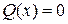 – линейным однородным.
– линейным однородным.
Линейные неоднородные уравнения могут быть решены методом Бернулли, который заключается в следующем. С помощью подстановки 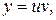 где
где 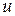 и
и 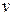 две неизвестные функции, исходное уравнение (III) преобразуется к виду
две неизвестные функции, исходное уравнение (III) преобразуется к виду
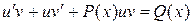 или
или 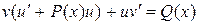 . (IV)
. (IV)
Так как одна из неизвестных функций может быть выбрана совершенно произвольно, за 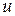 выбираем любое частное решение уравнения
выбираем любое частное решение уравнения 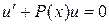 при этом из (IV) остаётся
при этом из (IV) остаётся
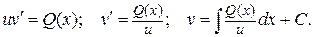
Общее решение исходного уравнения находится умножением 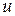 на v:
на v:
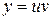 .
.
Пример. Проинтегрировать уравнение 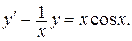
Решение. Данное уравнение является линейным уравнением первого порядка. Положим 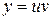 , тогда
, тогда 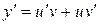 . Подставим
. Подставим 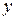 и
и 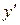 в данное уравнение
в данное уравнение 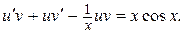 Сгруппируем члены, содержащие
Сгруппируем члены, содержащие 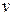 :
: 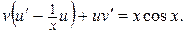 Подберём
Подберём 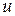 так, чтобы выражение в скобках обратилось в нуль:
так, чтобы выражение в скобках обратилось в нуль: 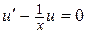 или
или 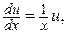 тогда
тогда 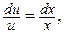 проинтегрировав, имеем
проинтегрировав, имеем 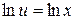 , т.е.
, т.е. 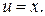 Решим оставшееся уравнение, подставив в него найденное
Решим оставшееся уравнение, подставив в него найденное 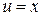 :
: 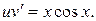
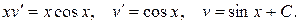
Общее решение данного уравнения имеет вид 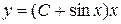 .
.
 2015-10-22
2015-10-22 252
252








