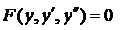
Уравнение приводится к уравнению первого порядка, если положить 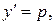 а за новый аргумент принять
а за новый аргумент принять 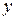 . В этом случае
. В этом случае 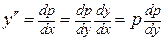 , и порядок уравнения понизился:
, и порядок уравнения понизился: 
Если его общее решение 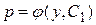 , т.е.
, т.е. 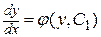 , то, разделяя переменные и интегрируя, найдем:
, то, разделяя переменные и интегрируя, найдем: 
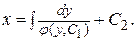
Пример. Проинтегрировать уравнение 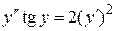 .
.
Решение. Понизим порядок этого уравнения, 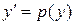 , тогда
, тогда 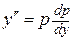 и получаем
и получаем 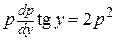 или
или  . Это дифференциальное уравнение распадается на два:
. Это дифференциальное уравнение распадается на два:  и
и 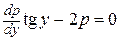 . Первое из них дает
. Первое из них дает 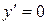 , т.е.
, т.е. 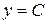 . Во втором переменные разделяются:
. Во втором переменные разделяются:  , откуда
, откуда  или
или  т.е.
т.е.  Вновь разделяя переменные, получим
Вновь разделяя переменные, получим  После интегрирования получим
После интегрирования получим  или
или  . Общее решение можно записать в виде
. Общее решение можно записать в виде  .
.
Отметим, что найденное выше решение 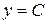 содержится в общем решении, так как получается из него при
содержится в общем решении, так как получается из него при 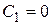 .
.
 2015-10-22
2015-10-22 575
575








