2015-10-22
208
Уравнение 
будем называть уравнением с разделяющимися переменными, если 
может быть разложено на множители, каждый из которых зависит только от одной переменной: 
.
(II)
Производную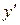 
можно рассматривать как отношение дифференциалов: 
, уравнение (II) примет вид 
Умножая обе части на 
и деля на 
, приведём уравнение к виду 
(переменные разделены). Интегрируя левую часть равенства по 
а правую часть по 
получаем общий интеграл (общее решение) уравнения (II): 
Пример. Найти общий интеграл уравнения 
Решение. Данное уравнение является уравнением с разделяющимися переменными. Запишем его в виде: 
. Разделим переменные, поделив почленно на 
и умножив на 
. Проинтегрируем: 
, 
Обозначим произвольную постоянную 
через 
, что допустимо, т.к. (при 
) может принимать любое значение от 
до 
. Следовательно, 
или 
– общий интеграл.
