2015-10-22
342
Из геометрического смысла определенного интеграла следует, что площадь криволинейной трапеции, ограниченной непрерывной кривой 
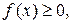двумя прямыми 
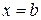и отрезком 
оси 
, вычисляется по формуле 
(I)
Если фигура ограничена непрерывными кривыми 
и 
, 
для всех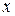 
, и прямым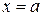и 
и 
то её площадь равна 
(II)
Если фигура заключена между кривыми и , то находим абсциссы точек пересечения данных кривых и вычисляем площадь фигуры по формуле (II).
Пример. Найти площадь фигуры, ограниченной параболами 
и 
.
Решение. Найдём абсциссы точек пересечения данных кривых: 
. По формуле (II):
Дифференциальные уравнения
Уравнения первого порядка
Основные понятия
Уравнение 
или 
(I)
связывающее независимую переменную х, искомую функцию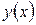 
и её производную 
называется дифференциальным уравнением первого порядка.
Решением дифференциального уравнения (I) называется такая дифференцируемая функция 
, которая при подстановке в уравнение обращает его в тождество.
Общим решением дифференциального уравнения (I) называется функция, зависящая от х и одной произвольной постоянной 
и обладающая следующими свойствами:
1) она является решением уравнения при любых значениях постоянной С,
2) для любого начального условия 
существует единственное 
, при котором решение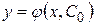 
удовлетворяет заданному начальному условию.
Всякое решение 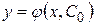, получающееся из общего решения при конкретном значении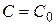 
, называется частным решением дифференциального уравнения.
