
Порядок такого уравнения можно понизить. Полагаем  тогда
тогда  . Для нахождения
. Для нахождения  имеем уравнение первого порядка
имеем уравнение первого порядка 
Пусть его общее решение  или
или  . Проинтегрировав, получим общее решение данного уравнения:
. Проинтегрировав, получим общее решение данного уравнения: 
Пример. Найти частное решение уравнения  если
если 

Решение. Данное уравнение – уравнение, не содержащее искомой функции. Положим  , тогда
, тогда  и уравнение примет вид:
и уравнение примет вид:  Это уравнение первого порядка с разделяющимися переменными:
Это уравнение первого порядка с разделяющимися переменными: 


 Возвращаясь к первоначальной функции, получим уравнение первого порядка
Возвращаясь к первоначальной функции, получим уравнение первого порядка  , из которого следует
, из которого следует 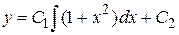 или
или  .
.
Подберем  и
и 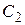 так, чтобы выполнились начальные условия. Поскольку
так, чтобы выполнились начальные условия. Поскольку 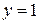 и
и  при
при  , то
, то  т.е.
т.е. 
 , т.е.
, т.е. 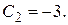 Искомое частное решение имеет вид
Искомое частное решение имеет вид 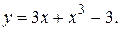
 2015-10-22
2015-10-22 315
315








