2015-10-22
265
В основе этой темы лежит понятие производной. Особое внимание следует обратить на геометрическое и механическое истолкование производной. Особую роль при решении задач играет правило вычисления производной сложной функции.
При дифференцировании некоторых функций нередко значительно упрощает вычисление прием, состоящий в том, что перед вычислением производной функцию предварительно логарифмируют.
При решении всех последующих примеров, кроме таблицы производных, используются правила дифференцирования суммы, разности, произведения, частного и теорема о производной сложной функции:
a) 
б) 
;
в)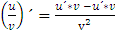 
;
г) 
Пример№1. Дана функция: y = 
.
Вычислить производную функции.
Решение:
y´=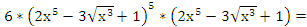 
= 
= 
.
Пример№2. Дана функция: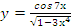 
Вычислить производную функции.
Решение:
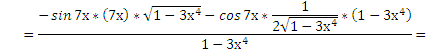
Пример №3. Дана функция: 
.
Вычислить производную функции.
Решение:
