Изучение этой темы следует начать с усвоения понятий возрастания и убывания функции, максимума и минимума функции, выпуклости и вогнутости кривой.
Пример:
1) Исследовать функцию у =  (х3 + 9х2 +15х - 9) и построить график.
(х3 + 9х2 +15х - 9) и построить график.
Решение:
1) D (x) = (-∞;+∞), т.е. функция непрерывна на всей числовой прямой.
2)Для исследования функции на экстремумы и монотонность необходимо найти производную и приравнять ее к нулю.
Имеем: y´ =  (3x2+9*2x + 15 − 0)
(3x2+9*2x + 15 − 0)
у' = 0 => 3х2+18х + 15= 0
х2+6х + 5 = 0
х1 = -5; х2 = -1
| х | (-∞,-5) | -5 | (-5;-1) | -1 | (-1;+∞) |
| f´(х) | + | 0 | − | 0 | + |
| f (x) | ↗ 
| max | ↘ | min | ↗ |
у max (-5)=  ((-5)3+9*(-5)2 +15*(-5) − 9) =4
((-5)3+9*(-5)2 +15*(-5) − 9) =4
у min (-1) =  ((-1)3 +9*(-1)2+15*(−1)−9) =−4
((-1)3 +9*(-1)2+15*(−1)−9) =−4
3) Для определения точек перегиба и интервалов вогнутости и выпуклости найдем вторую производную и приравняем ее к нулю.
Имеем: y ´´ =  (3 * 2 *x + 18+0)
(3 * 2 *x + 18+0)
6х + 18 = 0
х + 3 = 0
х = -3
| х | (-∞; -3) | -3 | (-3;+∞) |
| f ´(х) | - | 0 | + |
| f (x) | ∩ | точка перегиба | ∪ |
у(-3) =  ((-3)3 + 9(-3)2 + 15(−3) − 9) = 0.
((-3)3 + 9(-3)2 + 15(−3) − 9) = 0.
Точка (-3,0) - точка перегиба.
Используя полученные результаты исследования, построим график функции.

Тема «Интегралы»
Прежде чем приступить к интегрированию функций, тщательно изучите таблицу интегралов, свойства определенного интеграла и два простейших метода интегрирования: метод замены переменной и способ подстановки. Успех интегрирования в значительной степени зависит от того, сумеем ли мы подобрать удачную замену переменной, упрощающую данный интеграл.
При использовании метода интегрирования по частям очень важно правильно выбрать множители U и dv. Хотя общих правил разбиения нет, тем не менее, можно руководствоваться некоторыми частными правилами. Например, если подынтегральная функция представляет собой произведение показательной или тригонометрической функции и многочлена, то в качестве множителя U следует выбирать многочлен. Если же подынтегральная функция является произведением логарифмической или обратной тригонометрической функций и многочлена, то в качестве множителя U следует выбрать логарифмическую или обратную тригонометрическую функцию.
При интегрировании выражения, содержащего в знаменателе квадратный трехчлен, целесообразно привести этот трехчлен к виду с выделенным полным квадратом.
Пример№1. Найти интеграл: ∫(5 −  +2
+2 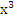 )dх.
)dх.
Решение: Воспользуемся таблицей интегралов и основными свойствами первообразной:
∫(5 −  +2
+2 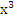 )dх = 5∫dх − 3∫
)dх = 5∫dх − 3∫  dх+2∫
dх+2∫ 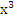 dх =
dх =
= 5х − 3tgх + 2  +с = 5х −3tgх +
+с = 5х −3tgх +  +с.
+с.
Пример №2. Найти интеграл: ∫ 
Решение: Воспользуемся определением степени с дробным показателем ( =
=  , а > 0), правилами действий со степенями с одинаковыми основаниями (аn am = an+m,
, а > 0), правилами действий со степенями с одинаковыми основаниями (аn am = an+m,  =
=  ), правилом деления суммы на число и найдем интеграл от каждого слагаемого отдельно.
), правилом деления суммы на число и найдем интеграл от каждого слагаемого отдельно.
∫  dх = ∫
dх = ∫  dх= ∫
dх= ∫  dх − ∫
dх − ∫  dх =
dх =
= 5∫х  dх − ∫х
dх − ∫х  dх = 5
dх = 5  −
−  +с = 3
+с = 3  −
−  +с =
+с =
= 3*  −
−  +с.
+с.
Пример №3. Найти интеграл: ∫  .
.
Решение: Применим подстановку: t = 
Тогда dt =  .
.
Имеем: ∫ ( = ∫
= ∫  dt =
dt =  (
( + c.
+ c.
Пример №4. Найти интеграл:
∫  dх.
dх.
Решение: Преобразуем знаменатель дроби, стоящей под знаком интеграла следующим образом:
х2 − 4х + 8 = х2 + 4 +7 = (х − 2)2 + 22.
Тогда после подстановки t= х−2 получаем:
∫  dх = ∫
dх = ∫  dх =∫
dх =∫  dt = ∫
dt = ∫  dt =
dt =
= ∫  dt +∫
dt +∫  dt =
dt =  (t2+4) +
(t2+4) +  actg
actg  +c =
+c =
 (х − 2
(х − 2  +4) +
+4) +  actg
actg  +c =
+c =
=  (х2 − 4х +8) +
(х2 − 4х +8) +  actg
actg  + с.
+ с.
При этом при вычислении интеграла ∫  dt мы воспользовались заменой переменной z = t2 +4.
dt мы воспользовались заменой переменной z = t2 +4.
Тогда dz = 2tdt, откуда
∫  dt =
dt =  ∫
∫  =
=  ∫
∫  =
=  c =
c =  (
( +4) +c.
+4) +c.
Пример №5. Найти интеграл: ∫(2х + 8)* 
Решение: Применим формулу интегрирования по частям: ∫udv=uv − ∫vdu.
Положим: u = 2х +8, dv = 
Тогда: du = 2dх, v = ∫  =
= 
Следовательно: ∫(2х + 8)  −
− 
 +
+ 
Пример №6. Найти интеграл: ∫actg3х*dх.
Решение: Положим u = actg3х, dv = dх, тогда du =  , v = х.
, v = х.
Отсюда: ∫actg3хdх = х* actg3х −3∫ 
Применим в последнем интеграле подстановку t = 1+9 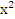 , получим dt=18хdх, следовательно: 3∫
, получим dt=18хdх, следовательно: 3∫  =
=  ∫
∫  =
=  (1+9
(1+9  )+с.
)+с.
Отсюда: ∫actg3хdх = х* actg3х −  (1+9
(1+9 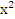 )+с.
)+с.
 2015-10-22
2015-10-22 575
575








