Производная функции комплексного переменного

предел отношения 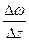= 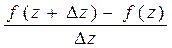, если 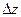любым способом стремится к нулю.

Таким образом,

.

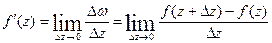Функция, имеющая производную при данном значении 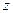, называется дифференцируемой (или моногенной) при этом значении 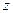. Если функция 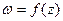однозначна и имеет конечную производную в каждой точке области D, то эта функция называется аналитической в области D.

Если функция 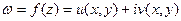дифференцируема в точке 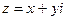, то в этой точке существуют частные производные 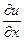, , 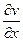, , 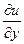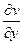причем эти производные связаны условиями

, ,

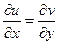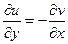которые называются условиями Коши-Римана.

Условия Коши-Римана являются необходимыми условиями дифференцируемости функции 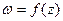в точке .

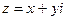Обратно, если частные производные 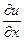, , 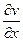, 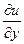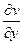непрерывны в точке 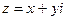и условия Коши-Римана 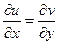, 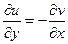выполнены, то функция 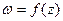дифференцируема в точке .

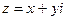Производная функции 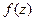выражается через частные производные функци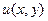й и 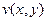по формулам

.

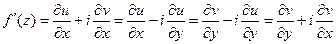Производные элементарных функций 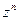, , 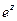, , 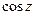, , 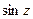, 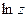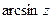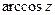arctg z, sh z, ch z находятся по тем же формулам, что и для действительного аргумента:

, ,

, ,

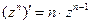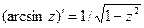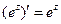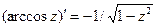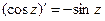, (arctg z ,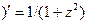

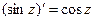, (sh 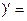z ch z,

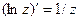, (ch z 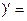sh z.