1. Основные определения. Пусть функция 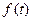 обладает следующими свойствами:
обладает следующими свойствами:
10.  при
при 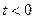 .
.
20. 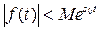 при
при  , где
, где 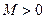 и s0-некоторые действительные постоянные.
и s0-некоторые действительные постоянные.
30. На любом конечном отрезке  положительной полуоси Ot функция
положительной полуоси Ot функция 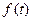 удовлетворяет условиями Дирихле, т.е.: а) ограничена; б) либо непрерывна, либо имеет лишь конечное число точек разрыва I рода; в) имеет конечное число экстремумов.
удовлетворяет условиями Дирихле, т.е.: а) ограничена; б) либо непрерывна, либо имеет лишь конечное число точек разрыва I рода; в) имеет конечное число экстремумов.
Такие функции в операционном исчислении называются изображаемыми по Лапласу, или оригиналами.
Пусть 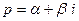 - комплексный параметр, причем Re
- комплексный параметр, причем Re 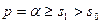 .
.
При сформулированных условиях интеграл 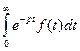 сходится и является функцией от p:
сходится и является функцией от p:
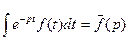 .
.
Этот интеграл называется интегралом Лапласа, а определяемая им функция комплексного аргумента p называется преобразованием Лапласа от функции 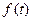 , или лапласовым изображением
, или лапласовым изображением 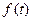 , или просто изображением
, или просто изображением 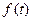 .
.
Тот факт, что функция 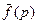 является изображением оригинала
является изображением оригинала 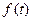 , обозначают следующими символами:
, обозначают следующими символами:
 , или
, или  .
.
Уславливаются за значение оригинала 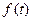 во всякой его точке разрыва I рода
во всякой его точке разрыва I рода 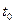 принимать полусумму его предельных значений слева и справа от этой точки:
принимать полусумму его предельных значений слева и справа от этой точки:
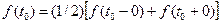 при
при  ;
;
 при
при  .
.
При соблюдении этого условия соответствие между оригиналами и изображениями обладает следующими свойствами:
это соответствие взаимно однозначно (т.е. всякому оригиналу соответствует единственное изображение и обратно),
любой линейной комбинации конечного множества оригиналов в качестве изображения отвечает соответствующая линейная комбинация их изображений.
Таким образом, если  (k = 1, 2, …, n), то
(k = 1, 2, …, n), то
 .
.
2. Нахождение изображений функций. В таблице и в каждом из приведенных ниже примеров указывается только значение 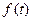 при
при 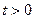 (всегда имеется в виду, что
(всегда имеется в виду, что 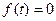 , если
, если 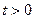 ).
).
| Таблица изображений основных элементарных функций | |||||
| № | 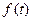 при при 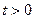
| 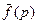
| № | 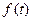 при при 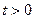
| 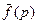
|
| I | 
| VI | 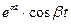
| 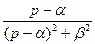
| |
| II | 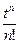
| 
| VII | 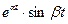
| 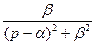
|
| III | 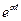
| 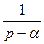
| VIII | 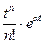
| 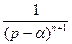
|
| IV | 
| 
| IX | 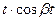
| 
|
| V | 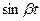
| 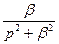
| X | 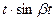
| 
|
 2015-10-22
2015-10-22 504
504








