Пусть дана функция 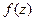 , аналитическая в некоторой окрестности точки
, аналитическая в некоторой окрестности точки  . Рассмотрим ряд
. Рассмотрим ряд
 .
.
Этот ряд называется рядом Тейлора функции 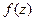 и внутри своего круга сходимости выражает функцию
и внутри своего круга сходимости выражает функцию 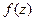 , т.е. в круге сходимости выполняется равенство
, т.е. в круге сходимости выполняется равенство
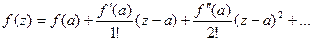 .
.
Если 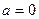 , то последнее равенство записывается в виде
, то последнее равенство записывается в виде
 .
.
В этом случае говорят, что функция 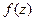 разложена в ряд Маклорена.
разложена в ряд Маклорена.
Рассмотрим теперь два ряда:
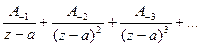 (1)
(1)
и
 (2)
(2)
Область сходимости первого ряда (если она существует) определяется неравенством  . Если существует область сходимости второго ряда, то она определяется неравенством
. Если существует область сходимости второго ряда, то она определяется неравенством 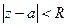 . Тогда при условии
. Тогда при условии 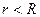 для ряда
для ряда
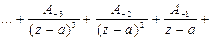
 ,
,
полученного сложением рядов (1) и (2), областью сходимости служит кольцо 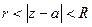 , ограниченное концентрическими окружностями с центром в точке
, ограниченное концентрическими окружностями с центром в точке  и радиусами
и радиусами 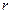 и
и 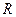 (см. рисунок).
(см. рисунок).
|
|

Пусть 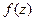 - однозначная и аналитическая функция в кольце
- однозначная и аналитическая функция в кольце 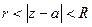 . Эта функция в указанном кольце может быть представлена в виде суммы ряда
. Эта функция в указанном кольце может быть представлена в виде суммы ряда

 .
.
Ряд в правой части равенства называется рядом Лорана функции 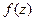 . Коэффициенты этого ряда можно вычислить по формуле
. Коэффициенты этого ряда можно вычислить по формуле

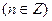
Ряд (1) называется главной частью ряда Лорана, а ряд (2) – правильной частью ряда Лорана.
Если ряд Лорана содержит главную часть, то  называется изолированной особой точкой. Коэффициент
называется изолированной особой точкой. Коэффициент  называется вычетом функции
называется вычетом функции 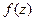 относительно изолированной особой точки
относительно изолированной особой точки 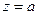 .
.
Особая точка называется устранимой, если функция 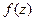 - аналитическая в окрестности
- аналитическая в окрестности 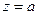 и ограничена по модулю в этой окрестности, т.е. существует конечный предел
и ограничена по модулю в этой окрестности, т.е. существует конечный предел 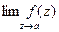 . Особая точка называется полюсом функции
. Особая точка называется полюсом функции 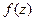 , если
, если 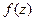 - аналитическая функция вблизи
- аналитическая функция вблизи 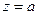 и стремится к бесконечности при
и стремится к бесконечности при 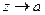 .
.
Особая точка 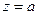 называется существенно особой, если при
называется существенно особой, если при 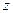 , близких к
, близких к  , модуль
, модуль 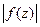 не остается ограниченным, но функция не стремится к
не остается ограниченным, но функция не стремится к 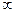 при
при 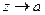 , предел
, предел 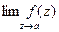 не существует.
не существует.
Изолированная особая точка является: устранимой, если главная часть разложения в ряд Лорана отсутствует. Например, для функции 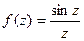 точка
точка 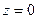 служит устранимой особой точкой, так как
служит устранимой особой точкой, так как
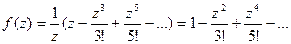 ;
;
Полюсом n -го порядка, если главная часть содержит конечное число членов, т.е. имеет вид

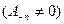 .
.
Например, для функции  точка
точка 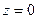 есть полюс первого порядка, так как
есть полюс первого порядка, так как
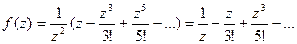 ;
;
Существенно особой, если главная часть содержит бесконечное число членов. Напримнр, функция 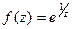 в точке
в точке 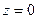 имеет существенно особую точку, так как
имеет существенно особую точку, так как
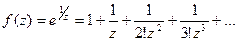 .
.
Между нулем и полюсом функции существует следующая связь. Если 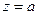 - нуль кратности
- нуль кратности 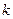 функции
функции 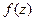 , то
, то 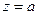 - полюс того же порядка функции
- полюс того же порядка функции 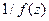 ; обратно, если
; обратно, если 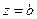 - полюс порядка
- полюс порядка 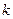 функции
функции 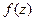 , то
, то 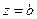 - нуль той же кратности функции
- нуль той же кратности функции 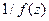 .
.
Следует заметить, что если  , то
, то 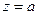 - полюс
- полюс 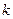 -го порядка функции
-го порядка функции 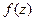 .
.
 2015-10-22
2015-10-22 2750
2750








