Рассмотрим линейное дифференциальное уравнение вида y′′+py′+q=0, где p, q − постоянные коэффициенты.
Для каждого такого дифференциального уравнения можно записать так называемое характеристическое уравнение: k2+pk+q=0.
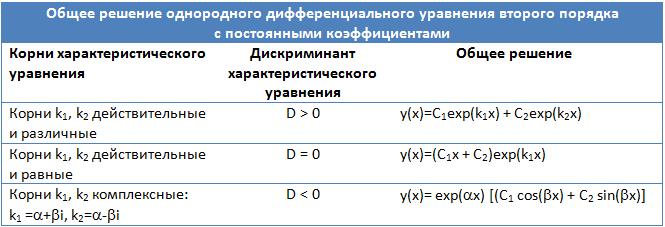
Общее решение однородного дифференциального уравнения зависит от корней характеристического уравнения, которое в данном случае будет являться квадратным уравнением. Возможны следующие три случая:
|
Пример 1. Найти частное решение дифференциального уравнения 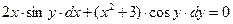 , если
, если 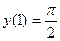
Решение: имеем уравнение с разделяющимися переменными. Разделим переменные, разделив каждый член уравнения на произведение 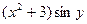 :
:
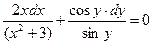
проинтегрируем обе части уравнения:
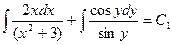
интегралы вычислим методом подстановки:
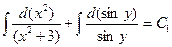
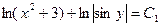
для удобства преобразований примем 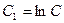 ,
,
тогда имеем 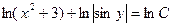
после потенцирования получаем общее решение:
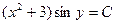
Подставив начальное условие 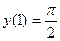 в общее решение, находим С
в общее решение, находим С
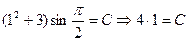
Подставляя найденное значение С в общее решение получаем частное решение.
Ответ: частное решение уравнения (частный интеграл) - 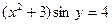 или
или 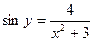
Пример 2. Найти частное решение дифференциального уравнения 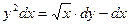 , если
, если 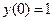 .
.
Решение: соберем члены, содержащие dx и dy в разных частях уравнения, а затем разделим переменные:
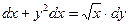
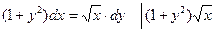
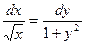
интегрированием найдем общее решение:
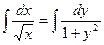
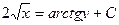
подставив начальное условие 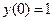 в общее решение, находим С:
в общее решение, находим С:
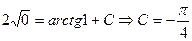
При найденном значении С из общего интеграла найдем частное решение (частный интеграл) данного уравнения: 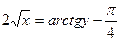
Ответ: частное решение 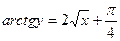
 2015-10-22
2015-10-22 686
686








