| № варианта | Определитель | № варианта | Определитель |
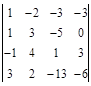
| 
|
| № варианта | Определитель | № варианта | Определитель |

| 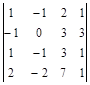
| ||
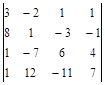
| 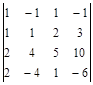
| ||
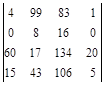
| 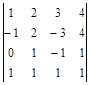
| ||
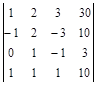
| 
|
Задача № 2. Даны матрицы А, В, С и числа 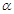 и
и 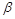 .
.
а) проверить, выполняются ли равенства:
1) (А + В) + С = А + (В + С) – сочетательный закон сложения матриц;
2) 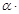 (
(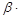 С) = (
С) = (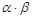 )
) 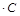 – сочетательный закон умножения матрицы на число;
– сочетательный закон умножения матрицы на число;
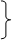
|
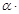 (А + В) =
(А + В) = 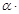 А +
А + 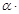 В
В
4) 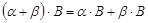
5) найти матрицу, равную 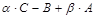 .
.
| № варианта | Матрица А | Матрица В | Матрица С | Числа | |
| α | 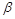
| ||||
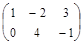
| 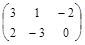
| 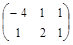
| – 2 | ||
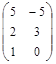
| 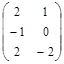
| 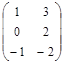
| – 3 | ||
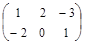
| 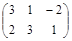
| 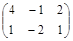
| – 2 | ||
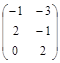
| 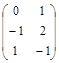
| 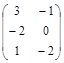
| – 3 | ||
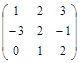
| 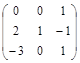
| 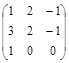
| – 2 | ||
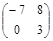
| 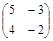
| 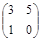
| – 3 | ||
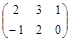
| 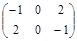
| 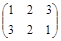
| – 3 | ||
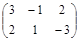
| 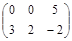
| 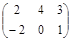
| – 2 | – 3 | |
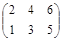
| 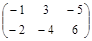
| 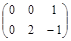
| – 2 | ||
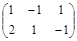
| 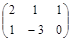
| 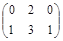
| – 1 |
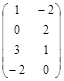
Задача № 3. Проверить, выполняется ли равенство 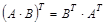 .
.
| № варианта | А | В | № варианта | А | В |
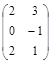
| 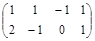
| 
| 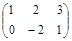
| ||
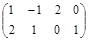
| 
| 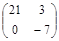
| 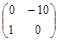
| ||
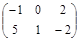
| 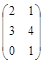
| 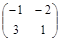
| 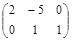
| ||
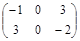
| 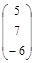
| 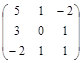
| 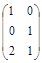
| ||
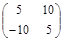
| 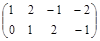
| 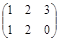
| 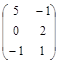
|
Задача № 4. Для данной матрицы найти обратную и убедиться, что обратная матрица найдена правильно.
| № варианта | Матрица | № варианта | Матрица |
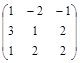
| 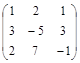
|
| № варианта | Матрица | № варианта | Матрица |
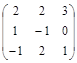
| 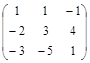
| ||
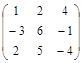
| 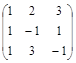
| ||
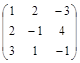
| 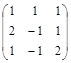
| ||
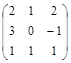
| 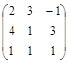
|
Задача № 5. Доказать, что система крамеровская, и решить систему указанным способом. Правильность решения доказать.
| № варианта | Решить по формулам Крамера систему | Решить матричным способом систему |
| № 1 | № 5 | |
| № 2 | № 7 | |
| № 3 | № 8 | |
| № 4 | № 10 | |
| № 5 | № 9 | |
| № 6 | № 1 | |
| № 7 | № 2 | |
| № 8 | № 3 | |
| № 9 | № 4 | |
| № 10 | № 6 |
№ 1 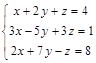
| № 6 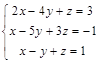
|
№ 2 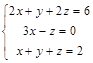
| № 7 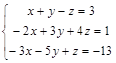
|
№ 3 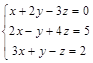
| № 8 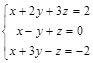
|
№ 4 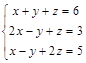
| № 9 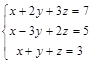
|
№ 5 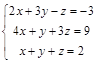
| № 10 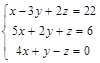
|
Задача № 6. Решить систему методом Гаусса.
| № варианта | Система | № варианта | Система |
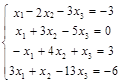
| 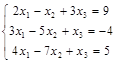
| ||
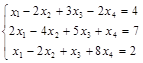
| 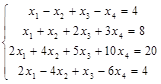
|
| № варианта | Система | № варианта | Система |
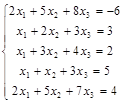
| 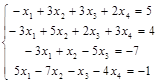
| ||
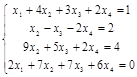
| 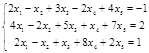
| ||
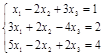
| 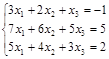
|
 2015-10-22
2015-10-22 673
673








