Второй замечательный предел служит для раскрытия неопределенности 1∞ и выглядит следующим образом

Обратим внимание на то, что в формуле для второго замечательного предела в показателе степени должно стоять выражение, обратное тому, которое прибавляется к единице в основании (так как в этом случае можно ввести замену переменных и свести искомый предел ко второму замечательному пределу).
Примеры.
1.  .
.
2. 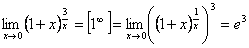 .
.
3.  .
.
4.  .
.
5.  .
.
 .
.
Правило Лопиталя раскрытия неопределенностей 0/0 и ∞/∞
Ранее мы познакомились с примерами нахождения пределов отношения двух бесконечно малых или бесконечно больших функций, то есть раскрытия неопределенностей вида 0/0 и ∞/∞. Сейчас рассмотрим новое правило раскрытия этих неопределенностей.
Теорема (правило Лопиталя). Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть  или
или  . Тогда, если существует предел отношения производных этих функций
. Тогда, если существует предел отношения производных этих функций  , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем
, то существует и предел отношения самих функций f(x)/g(x) при x→а, причем
 | ( |
Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.
Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.
Например, найти  . Этот предел существует
. Этот предел существует  . Но отношение производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому пределу.
. Но отношение производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому пределу.
Заметим, что если отношение производных опять представляет собой неопределенность вида 0/0 или ∞/∞, то можно снова применить сформулированную теорему, то есть перейти к отношению вторых производных и так далее.
1.  .
.
2.  .
.
Производная.
Пусть функция  определена на некотором промежутке X. Возьмём x из этого промежутка
определена на некотором промежутке X. Возьмём x из этого промежутка  дадим значению x приращение
дадим значению x приращение 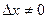 , тогда функция получит приращение
, тогда функция получит приращение 
Определение - производной функции  называют предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю, если этот предел существует.
называют предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю, если этот предел существует.




Другие обозначения: 
Нахождение производной функции называется дифференцирование. Функция дифференцируемая во всех точках на промежутке точек называется дифференцируемая на данном интервале.
1). основные правила дифференцирования:
· 
· 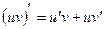
· 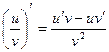
· 
2) формулы дифференцирования:
· 
· 
· 

· 

· 
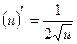
· 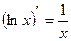

· 
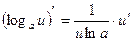
· 

· 

· 

· 

· 

· 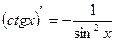

· 

· 
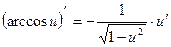
· 

· 
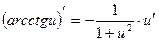
 2015-10-22
2015-10-22 5743
5743
