Скалярное произведение двух векторов

Определение. Скалярным произведением двух векторов и называется число, равное произведению длин векторов на косинус угла меду ними и обозначаемое

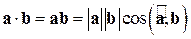или .

Если векторы и перпендикулярны, то их скалярное произведение . Обратно, если скалярное произведение векторов , то векторы и перпендикулярны.

Зная декартовы координаты векторов и

,

можно найти их длины

, ,

скалярное произведение

,

и косинус угла между ними

.

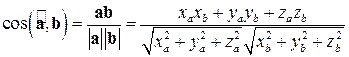Перечислим основные свойства векторного произведения:

1) 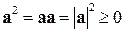, (из следует и обратно);

2) (переместительный закон);

3) (распределительный закон);

4) .