2015-10-22
343
Решение многих метрических задач связано с проведением перпендикулярных прямых и плоскостей и основывается на следующей теореме.
Теорема. Если одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то прямой угол на эту плоскость проекций проецируется в виде прямого же угла (рис. 74).
Рис. 74
Дано: 
; 
.
Требуется доказать: 
А1В1С1 = 900.
Доказательство:
ВС 
АВ по условию, ВС ВВ1 по построению (т.к. ВС 
П1, а ВВ1 П1). Следовательно ВС плоскости Γ (АВ ∩ ВС).
ВС В1С1, поэтому В1С1 Γ.
Следовательно, В1С1 будет перпендикулярна прямой А1В1 = Γ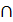 
П1, т.е. А1В1С1 = 900.
Из доказанной теоремы вытекает следствие: если прямая n перпендикулярна плоскости Δ = h 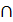f, то горизонтальная проекция этой прямой перпендикулярна горизонтальной проекции горизонтали плоскости (n1 h1), а фронтальная проекция n2 перпендикулярна фронтальной проекции f2 фронтали этой плоскости. В самом деле, так как h П1, а f П2, то на основании предыдущей теоремы n1 будет перпендикулярна h1, а n2 будет перпендикулярна f2 (рис. 75).
Рис. 75
Задача. Найти расстояние от точки D до плоскости ΔАВС.
Решение задачи состоит из трех этапов:
1. На основании предыдущего следствия из точки D (D1, D2) проводим перпендикуляр n: n1 h1 и n2 f2 (рис. 76).
2. Строим точку К пересечения этого перпендикуляра с плоскостью АВС (первая основная позиционная задача).
3. Находим натуральную величину отрезка DK (D1К1, D2К2) способом прямоугольного треугольника.
Рис. 76
