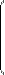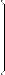2015-10-22
6210
Этот метод заключается в том, что исходный определитель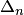 
n-го порядка выражается через определители 
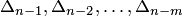того же вида, но меньшего порядка. Получается рекуррентное уравнение
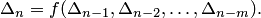
Решая это уравнение, находим формулу, выражающую определитель 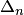через определители 
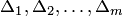и порядок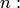 
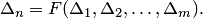
В последнюю формулу подставляем определители 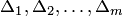невысокого 
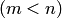порядка, которые нетрудно вычислить каким-либо другим способом.
Треугольная матрица
Треугольная матрица — в линейной алгебре квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю.
Пример верхнетреугольной матрицы
Верхнетреугольная матрица — квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.
Нижнетреугольная матрица — квадратная матрица, в которой все элементы выше главной диагонали равны нулю.
Унитреугольная матрица (верхняя или нижняя) — треугольная матрица, в которой все элементы на главной диагонали равны единице.
Треугольные матрицы используются в первую очередь при решении линейных систем уравнений, когда матрица системы сводится к треугольному виду используя следующую теорему:
|
|
|
Любую ненулевую матрицу 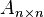 путём элементарных преобразований над строками и перестановкой столбцов можно привести к треугольному виду.
|
| Любая квадратная матрица, имеющая отличные от нуля главные миноры, представима произведением двух матриц: верхнетреугольной, и нижнетреугольной. Разложение единственно, если фиксированы (заранее оговорены) элементы главной диагонали одной из них. |
Решение систем линейных уравнений с треугольной матрицей (обратный ход) не представляет сложностей.
Свойства
- Определитель треугольной матрицы равен произведению элементов на её главной диагонали.
- Определитель унитреугольной матрицы равен единице.
- Множество невырожденных верхнетреугольных матриц порядка n по умножению с элементами из поля k образует группу, которая обозначается UT (n, k) или UT n (k).
- Множество невырожденных нижнетреугольных матриц порядка n по умножению с элементами из поля k образует группу, которая обозначается LT (n, k) или LT n (k).
- Множество верхних унитреугольных матриц с элементами из поля k образует подгруппу UT n (k) по умножению, которая обозначается SUT (n, k) или SUT n (k). Аналогичная подгруппа нижних унитреугольных матриц обозначается SLT (n, k) или SLT n (k).
- Множество всех верхнетреугольных матриц с элементами из кольца k образует алгебру относительно операций сложения, умножения на элементы кольца и перемножения матриц. Аналогичное утверждение справедливо для нижнетреугольных матриц.
Определение.
Минором Mij к элементу aij определителя n-го порядка называется определитель (n - 1)-го порядка, полученный из исходного определителя вычеркиванием i-той строки и j-того столбца.
|
|
|
Пример 1.
Найти миноры матрицы A
| A = |
|
Решение:
| M22 = |
| = |
| M11 = | = 1·3 - 0·0 = 3 - 0 = 3 |
| M12 = |
| = -4·3 - 0·2 = -12 -0 = -12 |
| M13 = |
| = -4·0 - 1·2 = 0 - 2 = -2 |
| M21 = | = 7·3 - 1·0 = 21 - 0 = 21 |
| M22 = | = 5·3 - 1·2 = 15 - 2 = 13 |
| M23 = | = 5·0 - 7·2 = 0 - 14 = -14 |
| M31 = | = 7·0 - 1·1 = 0 - 1 = -1 |
| M32 = |
| = 5·0 - 1·(-4) = 0 + 4 = 4 |
| M33 = |
| = 5·1 - 7·(-4) = 5 + 28 = 33 |
Определение.
Алгебраическим дополнением Aij к элементу aij определителя n-го порядка называется число
Aij = (-1)i + j · Mij
