При вычислении определителей бывает полезно изменить все его элементы, умножив их на одно и то же число, не равное нулю, либо прибавить к каждому элементу одно и то же число. Найдем формулы изменения определителя при этих преобразованиях.
Пусть дана квадратная матрица 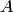 n-го порядка. Из свойства 6 следует, что при умножении всех элементов определителя n-го порядка на число
n-го порядка. Из свойства 6 следует, что при умножении всех элементов определителя n-го порядка на число 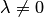 определитель умножается на число
определитель умножается на число 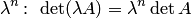 .
.
Рассмотрим теперь определитель матрицы  , элементы которой
, элементы которой  получены из соответствующих элементов матрицы
получены из соответствующих элементов матрицы 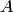 прибавлением числа
прибавлением числа 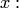
Применяя свойство 7 к первому столбцу этого определителя, получаем сумму определителей
То же свойство применяем к каждому определителю ("раскладывая" второй столбец) и т.д. В итоге получим сумму 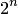 определителей n-го порядка, причем определители, имеющие по два и более столбцов из элементов, равных
определителей n-го порядка, причем определители, имеющие по два и более столбцов из элементов, равных 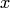 , равны нулю (по свойству 4). Поэтому в сумме остаются только
, равны нулю (по свойству 4). Поэтому в сумме остаются только 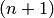 слагаемых: определитель матрицы
слагаемых: определитель матрицы 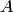 и
и 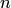 определителей вида
определителей вида
отличающихся от определителя матрицы 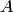 только j-м столбцом. Раскладывая этот определитель по j-му столбцу, получаем сумму алгебраических дополнений элементов этого столбца, умноженную на
только j-м столбцом. Раскладывая этот определитель по j-му столбцу, получаем сумму алгебраических дополнений элементов этого столбца, умноженную на 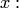
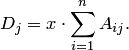
Следовательно, сумма всех таких определителей  равна сумме алгебраических дополнений всех элементов матрицы
равна сумме алгебраических дополнений всех элементов матрицы 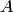 , умноженной на
, умноженной на 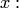

Окончательно получаем, что при увеличении всех элементов определителя на число 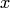 , определитель увеличивается на сумму всех алгебраических дополнений, умноженную на число
, определитель увеличивается на сумму всех алгебраических дополнений, умноженную на число 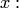
Пример 2.14. Вычислить определитель n-го порядка
Решение. Рассмотрим определитель диагональной матрицы 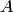
Искомый определитель  получается прибавлением к каждому элементу определителя матрицы
получается прибавлением к каждому элементу определителя матрицы 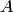 числа
числа 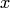 . Поэтому
. Поэтому
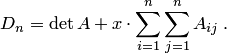
Определитель диагональной матрицы 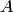 равен произведению диагональных элементов:
равен произведению диагональных элементов:
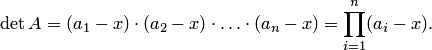
Осталось вычислить сумму алгебраических дополнений всех элементов матрицы 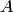 . Заметим, что алгебраическое дополнение недиагонального элемента равно нулю (
. Заметим, что алгебраическое дополнение недиагонального элемента равно нулю (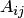 при
при 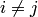 , так как дополнительный минор содержит нулевой столбец). Дополнительный минор диагонального элемента — это определитель диагональной матрицы, т.е.
, так как дополнительный минор содержит нулевой столбец). Дополнительный минор диагонального элемента — это определитель диагональной матрицы, т.е.
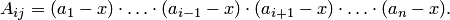
Поэтому
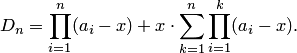
 2015-10-22
2015-10-22 2256
2256
