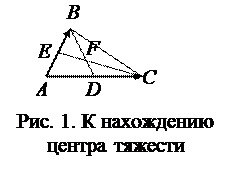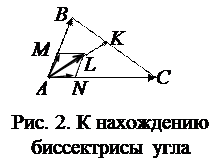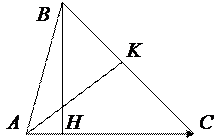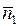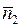МАТЕМАТИКА
ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
(типовой расчет)
Методические указания и контрольные задания
для самостоятельной работы студентов
горных специальностей очной формы обучения
Составитель М. К. Курчин
Утверждено на заседании кафедры
Протокол № 9 от 08.04.2009
Рекомендовано к печати
учебно-методической комиссией
специальности 130403
Протокол № 10 от 27.04.2009
Электронная копия хранится
в библиотеке главного корпуса
ГУ КузГТУ
Данная работа служит качественному выполнению типового расчета студентами первого курса в первом учебном семестре по темам «линейной алгебры» и «аналитической геометрии». В качестве основного учебника рекомендуется «Курчин М. К. Алгебра и геометрия для инженеров: Учеб. пособие / ГУ КузГТУ. – Кемерово, 2004. – 158с.» Именно, по этому учебнику указаны в приводимых решениях задач параграфы для самостоятельной работы. Методические указания содержат пример выполнения типового расчета (из шести задач) и контрольные задания в количестве 36 вариантов. В конце методических указаний приведены ответы ко всем задачам.
Пример выполнения типового расчета
Задача 1. Решить систему 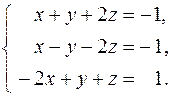
а) методом последовательного исключения неизвестных;
б) методом определителей; в) матричным методом.
Решение. а) Нам следует (§1) выписать матрицу из коэффициентов системы, присоединить к ней столбец из свободных членов, для удобства отделенный вертикальной чертой, и все преобразования выполнять над строками этой расширенной матрицы.
Подвергнем преобразованиям расширенную матрицу этой системы: 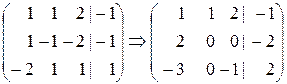 . Дальнейшие преобразования расширенной матрицы не требуются.
. Дальнейшие преобразования расширенной матрицы не требуются.
Мы приходим, следовательно, к системе уравнений
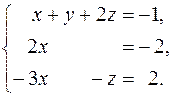 или
или 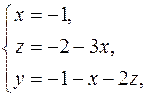
обладающей единственным решением х = –1, y = -2, z = 1.
Исходная система оказалась определенной.
б). Для нашей системы (§5 и §6) вычисляем все нужные определители. Здесь:
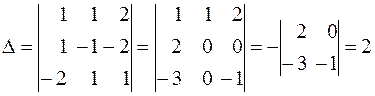 ,
,
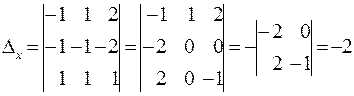 ,
,
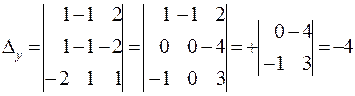 ,
,
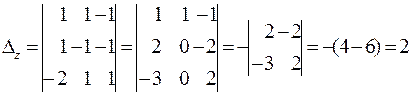 ,
,
Теперь находим 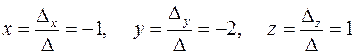 .
.
в) Матрица из коэффициентов при неизвестных будет:
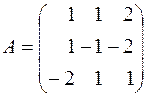 . Ее определитель D = | А | = 2, поэтому обратная матрица А -1 существует (§44 и §45), причем
. Ее определитель D = | А | = 2, поэтому обратная матрица А -1 существует (§44 и §45), причем
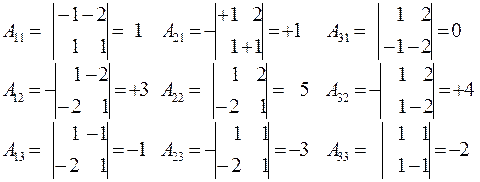
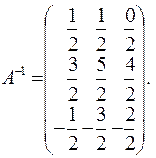
Матрица-столбец из свободных членов уравнений системы будет: 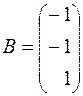 . Решением системы будет матрица:
. Решением системы будет матрица:
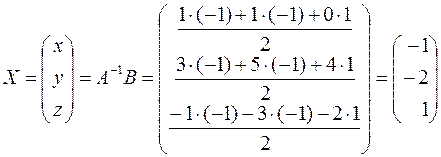 , т. е.
, т. е. 
|
Задача 2. Вершины треугольника находятся в точках A (–5; 1; 3), B (–5; 4; 7) и C (5; –4; –7). Найти координаты центра тяжести треугольника, величину угла А и направляющие косинусы биссектрисы этого угла.
Решение. Для того чтобы найти координаты точки F – центр тяжести треугольника, заметим, что она делит медиану BD в отношении 2:1, считая от вершины B, а точка D делит сторону AD пополам (§§7-15). Найдем координаты точки D, для чего воспользуемся формулами деления отрезка пополам:
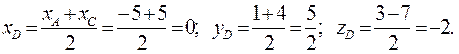
Итак, 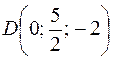 и точка F делит отрезок BD в отношении
и точка F делит отрезок BD в отношении
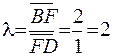 .
.
Находим координаты точки F:
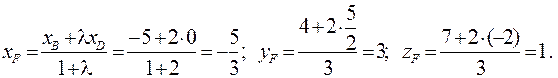
А центр тяжести треугольника находится в точке 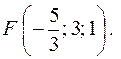
Для того чтобы найти величину угла А, укажем векторы (рис.1)
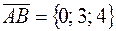 и
и 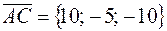
(из координат конца вычитаем координаты начала) и найдем их длины:
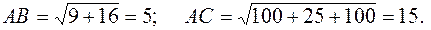
Тогда 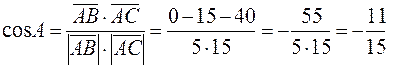 ,
,
а сам угол А будет равен»37,17 градусам.
Направляющие косинусы биссектрисы угла А можно найти двумя способами. Рассмотрим их.
1 способ. Биссектриса внутреннего угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам. На основании этого, заключаем, что точка K делит отрезок СВ в отношении 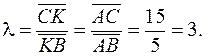
Находим координаты точки K:
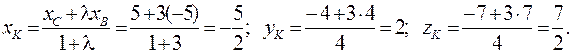
|
так, 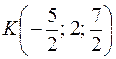 и вектор биссектрисы
и вектор биссектрисы
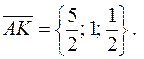
Его длина 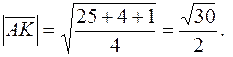
Тогда 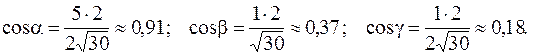
2 способ. По направлениям векторов 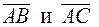 рассмотрим единичные векторы
рассмотрим единичные векторы
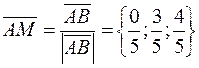 и
и 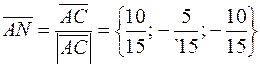 .
.
Если сложить эти векторы, то параллелограмм AMLN будет являться в то же время и ромбом, а его диагональ AL будет биссектрисой угла А. Следовательно, 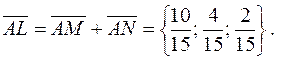
Найдем длину этого вектора: 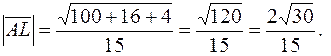
Тогда 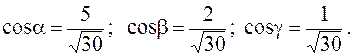
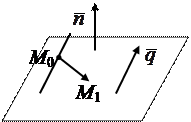
Задача 3. Вычислить расстояние от точки K (2; –1; –2) до плоскости Р, проходящей через точку M 1(3; –3; –5) и прямую 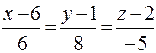 , и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
Решение. Заданная прямая проходит через точку M 0(6; 1; 2) параллельно вектору 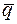 = {6; 8; –5} (§27, задача 4). Найдем вектор
= {6; 8; –5} (§27, задача 4). Найдем вектор 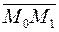 ={–3; –4; –7}. Нормальный вектор
={–3; –4; –7}. Нормальный вектор 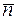 плоскости Р перпендикулярен векторам
плоскости Р перпендикулярен векторам 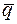 и
и 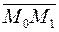 , так что в качестве нормального вектора
, так что в качестве нормального вектора 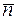 можно взять векторное произведение векторов
можно взять векторное произведение векторов 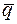 и
и 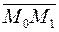 .
.
|
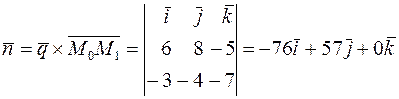 .
.
Нам удобнее взять за вектор  , вектор в –19 раз короче, т. е.
, вектор в –19 раз короче, т. е.  = {4; –3; 0}. Теперь запишем уравнение плоскости, проходящей через точку M 1 перпендикулярно вектору
= {4; –3; 0}. Теперь запишем уравнение плоскости, проходящей через точку M 1 перпендикулярно вектору 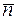 :
:
4(x – 3) – 3(y + 3) = 0, P: 4 x – 3 y – 21 = 0.
Остается вычислить расстояние точки K от плоскости Р:
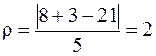 .
.
И записать уравнение перпендикуляра, опущенного из точки K на плоскость Р:
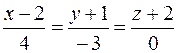 .
.
Задача 4. Даны уравнения х – 2 у – 1 = 0, х + 3 у – 6 = 0 и 3 х – у + 2 = 0 двух сторон треугольника и медианы. Составить уравнения третьей стороны треугольника и его высоты, опущенной на эту сторону.
Решение. Пусть уравнения сторон
AB: х – 2 у – 1 = 0 и BC: х + 3 у – 6 = 0.
Находим (§28) координаты вершины B: 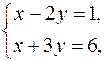
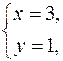 B (3; 1).
B (3; 1).
Координаты вершины B уравнению медианы не удовлетворяют: 3·3 – 1 – 6 ¹ 0. Пусть медиана проведена из вершины A к стороне BC. Найдем координаты вершины
|
A: 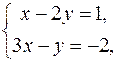
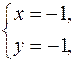 A (–1; –1).
A (–1; –1).
Найдем теперь координаты точки K пересечения медианы AK со стороной BC:
K: 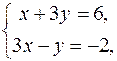
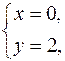 K (0; 2).
K (0; 2).
Точка C делит отрезок BK внешним образом в отношении 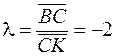 .
.
Следовательно, 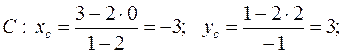 C (–3; 3).
C (–3; 3).
Вектор 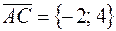 , а уравнение стороны AC, как проходящей через точку A, параллельно вектору
, а уравнение стороны AC, как проходящей через точку A, параллельно вектору 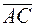 , запишется:
, запишется:
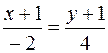 или 2 x + y + 3 = 0.
или 2 x + y + 3 = 0.
Высота BH проходит через вершину B и в качестве нормального вектора можно взять вектор 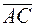 . Тогда ее уравнение запишется:
. Тогда ее уравнение запишется:
–2(x – 3) + 4(y – 1) = 0 или x – 2 y – 1 = 0.
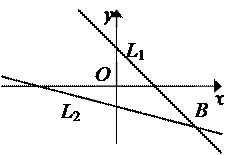
Задача 5. Через точку В (8; -3 ) провести прямую так, чтобы площадь треугольника, образованного ею и осями координат, была равна одной квадратной единице.
Решение. Уравнение прямой возьмем в виде уравнения прямой в отрезках 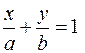 , где а и b – величины отрезков, отсекаемых прямой на координатных осях (§28).
, где а и b – величины отрезков, отсекаемых прямой на координатных осях (§28).
|
Задача имеет 2 решения. Одна прямая L 1 пересекает первый координатный угол, для которого a > 0, b > 0 и ab > 0. Другая прямая L 2 пересекает третий координатный угол, для которого a < 0, b < 0 и ab > 0.
Площадь треугольника 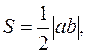 а так как у нас в любом случае
а так как у нас в любом случае
 то
то 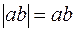 и
и 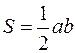 .
.
К тому же искомая прямая проходит через точку В и координаты последней удовлетворяют уравнению прямой.
Таким образом, по условию задачи имеем систему 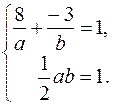
Решаем эту систему:
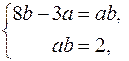 или
или 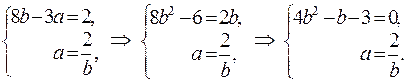
Решением этой системы будут две пары значений:
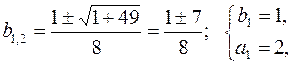 и
и 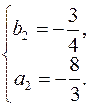
Следовательно, искомые прямые имеют уравнения:
 
        ` `
   • • |
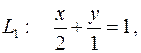 или x + 2 y – 2 = 0;
или x + 2 y – 2 = 0;
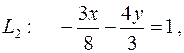 или 9 x + 32 y – 24 = 0.
или 9 x + 32 y – 24 = 0.
Ответ: х + 2 у -2 = 0; 9 х +32 у –24 = 0.
Задача 6. Из точки B (4; 0) направлен луч под углом arctg 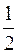 к прямой x – 2 y + 6 = 0. Найти уравнение луча, отраженного от этой прямой.
к прямой x – 2 y + 6 = 0. Найти уравнение луча, отраженного от этой прямой.
Решение. 1). Пусть падающий луч направлен по прямой BA, так что угол BAC равен φ = arctg 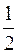 . Нормальный вектор заданной прямой x – 2 y + 6 = 0 будет
. Нормальный вектор заданной прямой x – 2 y + 6 = 0 будет 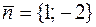 и вектор
и вектор 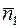 , нормальный вектор падающего луча – прямой BA, получается поворотом вектора
, нормальный вектор падающего луча – прямой BA, получается поворотом вектора 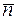 против часовой стрелки на угол φ. Воспользуемся формулами вычисления координат вектора, получающегося путем поворота против часовой стрелки данного вектора на некоторый угол (§20):
против часовой стрелки на угол φ. Воспользуемся формулами вычисления координат вектора, получающегося путем поворота против часовой стрелки данного вектора на некоторый угол (§20):
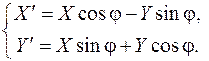 (1)
(1)
В качестве вектора 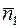 можно взять растянутый вектор
можно взять растянутый вектор 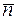 , т. е.
, т. е. 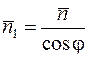 . Формулы (1) тогда примут вид:
. Формулы (1) тогда примут вид:
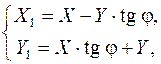 или с данными задачи
или с данными задачи 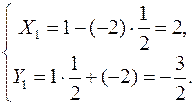
Чтобы координаты вектора задавались целыми числами, возьмем вектор 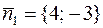 .
.
Найдем уравнение прямой AB, проходящей через точку B и имеющей нормальный вектор 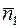 (§28):
(§28):
4(x – 4) –3(y –0) = 0 или 4 x – 3 y = 16.
Находим координаты точки A: 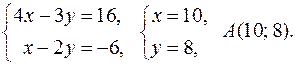
Для отраженного луча нормальный вектор 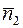 может быть получен поворотом вектора
может быть получен поворотом вектора 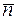 на тот же угол φ, но теперь по часовой стрелке. Заменяя в формулах вычисления координат преобразованного вектора угол φ на угол –φ, получим систему:
на тот же угол φ, но теперь по часовой стрелке. Заменяя в формулах вычисления координат преобразованного вектора угол φ на угол –φ, получим систему:
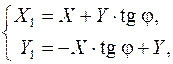 или с данными задачи
или с данными задачи 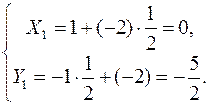
Чтобы координаты вектора задавались целыми числами, возьмем вектор 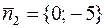 . Тогда уравнение отраженного луча запишется:
. Тогда уравнение отраженного луча запишется:
0(x – 10) – 5(y – 8) = 0 или y = 8.
2). Пусть теперь падающий луч направлен по прямой BC, так что угол BCA равен φ = arctg 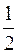 . Нормальный вектор заданной прямой x – 2 y + 6 = 0 будет
. Нормальный вектор заданной прямой x – 2 y + 6 = 0 будет 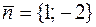 и вектор
и вектор 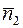 , нормальный вектор падающего луча – прямой BC, получается поворотом вектора
, нормальный вектор падающего луча – прямой BC, получается поворотом вектора 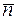 против часовой стрелки на угол π – φ, что равносильно – с точностью до выбора направления – повороту вектора
против часовой стрелки на угол π – φ, что равносильно – с точностью до выбора направления – повороту вектора 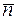 по часовой стрелке на угол φ. Но это и будет как раз вектор
по часовой стрелке на угол φ. Но это и будет как раз вектор 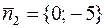 . Уравнение падающего луча BC запишется: 0(x – 4) – 5(y – 0) = 0 или y = 0. Тогда С (–6; 0) и для отраженного луча нормальный вектор будет
. Уравнение падающего луча BC запишется: 0(x – 4) – 5(y – 0) = 0 или y = 0. Тогда С (–6; 0) и для отраженного луча нормальный вектор будет 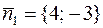 . Наконец, уравнение отраженного луча запишется: 4(x + 6) – 3(y – 0) = 0 или 4 x – 3 y + 24 = 0.
. Наконец, уравнение отраженного луча запишется: 4(x + 6) – 3(y – 0) = 0 или 4 x – 3 y + 24 = 0.
Ответ: 1) y = 8; 2) 4 x – 3 y + 24 = 0.
1. Линейная алгебра.
Решить систему линейных уравнений а) методом последовательного исключения неизвестных; б) методом определителей; в) матричным методом.
1. 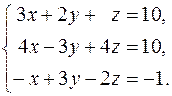 2.
2. 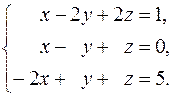 3.
3. 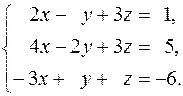
4. 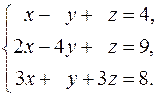 5.
5. 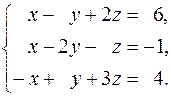 6.
6. 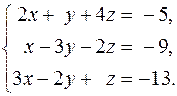
7. 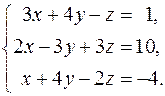 8.
8. 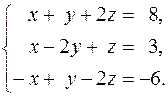 9.
9. 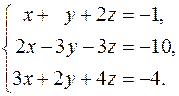
10. 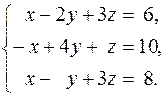 11.
11. 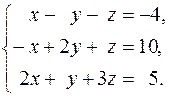 12.
12. 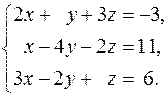
13. 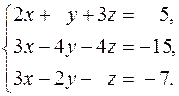 14.
14. 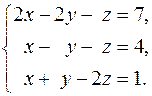 15.
15. 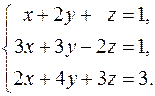
16. 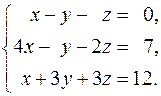 17.
17. 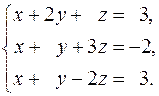 18.
18. 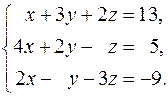
19. 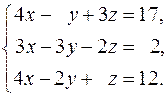 20.
20. 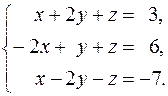 21.
21. 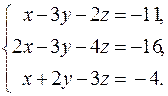
22. 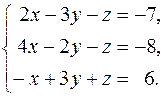 23.
23. 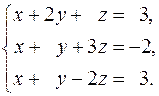 24.
24. 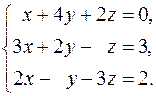
25. 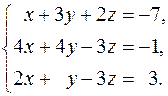 26.
26. 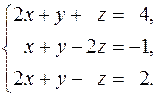 27.
27. 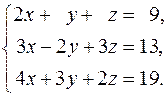
28. 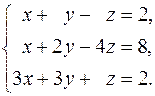 29.
29. 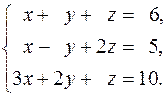 30.
30. 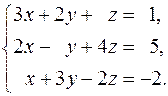
31. 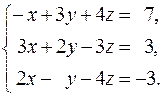 32.
32. 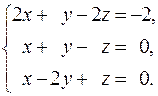 33.
33. 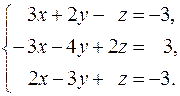
34. 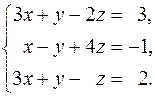 35.
35. 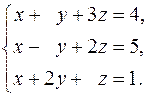 36.
36. 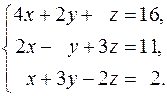
2. Векторная алгебра.
Вершины треугольника находятся в точках А, В и С. Найти координаты центра тяжести треугольника, направляющие косинусы биссектрисы угла А и величину этого угла.
| вариант | ||||||
| A | –4;–2;–4 | –4; 2; –2 | –1; 2; –8 | –6; 3; –2 | –8; 2; –4 | –3; –2; –2 |
| B | –3; 2; 4 | 4; –6; 2 | –3; –6; 8 | –6; 6; 2 | –7; 6; 4 | 4; 2; 2 |
| C | 4; 2; 4 | –2; 6; 2 | 3; 6; –1 | 6; –6; –2 | 8; –6; –2 | –1; 2; 2 |
| вариант | ||||||
| A | 2; –1; –1 | –5; 3; –2 | 7; 2; 0 | –1; 3; –5 | –8; 2; –3 | 5; –6; –4 |
| B | 1; –3; –3 | 6; –7; –4 | –7; –6; –8 | 1; 7; –1 | –4; 6; 4 | –5; 5; –6 |
| C | –2; 3; –3 | –2; 9; 4 | 8; 6; 8 | 1; –7; 6 | 8; –6; –5 | 5; 0; 4 |
| вариант | ||||||
| A | 4; –1; 4 | –6; –4; 2 | –2; 1; –1 | 6; –3; –4 | 4; 5; 0 | 3; –2; –1 |
| B | –4;–3;–12 | –8; 0; 6 | 2; –3; 1 | –10;–5; 4 | 5; 9; 8 | 5; 2; 3 |
| C | 5; 3; 12 | 8; 4; –6 | –1; 3; 1 | 10; 5; 4 | –4;–9;–8 | –5; 2; –2 |
| вариант | ||||||
| A | 5; 2; 1 | –6;–6;–3 | 1; –8; –4 | –6; 1; –2 | –1;–4;–8 | –7;–4;–3 |
| B | –9;–6;–7 | –3; 0; 3 | –1; 8; 4 | –4; 5; 2 | 1; 4; 8 | –3; 4; 5 |
| C | 9; 6; 8 | 6; 6; 3 | 2; –4; 4 | 6; –5; 2 | 0;–2;–6 | 7; 4; 5 |
| вариант | ||||||
| A | 4; 2; –7 | –1;–4;–8 | 0;–3;–4 | 5; –1; 4 | –1; –8; 1 | 3; –3; 1 |
| B | 5; 6; 1 | 1; 4; 8 | 3; –3; 0 | 6; 1; 6 | –3; 8; –7 | 7; 5; 9 |
| C | –4; –6; 7 | 1; 0; –4 | 0; 3; 4 | –6; 1; –6 | 3; –4; 8 | –7;–5;–10 |
| вариант | ||||||
| A | –5;–6;–4 | –1; 4; 3 | 4; –8; –4 | 3; 1; –2 | –2; 2; –6 | –8;–1;–4 |
| B | 4; 6; –4 | 1; –7; –7 | 5; –4; 4 | –4; –3; 2 | 2; 6; 1 | –7; 3; 4 |
| C | –4; –2; 4 | –1; 7; 7 | –4; 8; –2 | 4; 3; 0 | –2; –7; 6 | 8; –3; 4 |
3. Плоскость и прямая в пространстве.
1. Вычислить расстояние от точки K (–5; 3; –2) до плоскости Р, проходящей через точку M 0(3; 2; 4) параллельно вектору 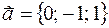 и перпендикулярно плоскости 4 x + y – 3 z – 7 = 0, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
и перпендикулярно плоскости 4 x + y – 3 z – 7 = 0, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
2. Вычислить расстояние от точки K (1; –1; 4) до плоскости Р, проходящей через точку M 0(–2; –5; 3) перпендикулярно прямой 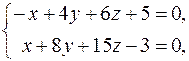 и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
3. Вычислить расстояние от точки K (–3; 0; 1) до плоскости Р, проходящей через прямую 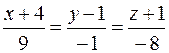 параллельно вектору
параллельно вектору 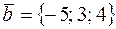 , и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
4. Вычислить расстояние от точки K (1; 1; 5) до плоскости Р, проходящей через точку M 0(2;–1;–3) перпендикулярно двум плоскостям 5 x – 2 y + 12 z + 4 = 0 и 10 x + 7 y + 24 z – 2 = 0, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
5. Вычислить расстояние от точки K (2; 5; 3) до плоскости Р, проходящей через точку M 0(–4; 3; –1) параллельно двум прямым 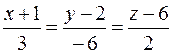 и
и 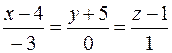 , и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
6. Вычислить расстояние от точки K (4; –1; –2) до плоскости Р, проходящей через прямую 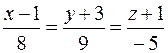 перпендикулярно плоскости –4 x + 7 z + 3 = 0, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
перпендикулярно плоскости –4 x + 7 z + 3 = 0, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
7. Вычислить расстояние от точки K (4; 1; 3) до плоскости Р, проходящей через две точки M 1(5; 3; –4) и M 2(–8; 4; 8) параллельно вектору 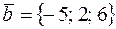 , и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
8. Вычислить расстояние от точки K (4; –5; –2) до плоскости Р, проходящей через две параллельные прямые 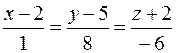 и
и 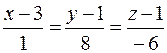 , и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
9. Вычислить расстояние от точки K (1; –2; 3) до плоскости Р, проходящей через точку M 0(4; –3; 1) параллельно двум векторам 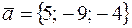 и
и 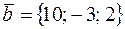 , и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
10. Вычислить расстояние от точки K (1; –1; 0) до плоскости Р, проходящей через точку M 0(5; 2; –2) и прямую 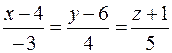 , и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
11. Вычислить расстояние от точки K (2; –1; –2) до плоскости Р, проходящей через точку M 0(2; –4; 0) параллельно вектору 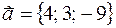 и перпендикулярно плоскости y + 3 z + 4 = 0, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
и перпендикулярно плоскости y + 3 z + 4 = 0, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
12. Вычислить расстояние от точки K (3; 1; 2) до плоскости Р, проходящей через точку M 0(–4; –5; 1) перпендикулярно прямой 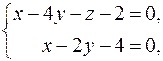 и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
13. Вычислить расстояние от точки K (2; –3; 4) до плоскости Р, проходящей через прямую 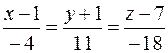 параллельно вектору
параллельно вектору 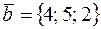 , и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
14. Вычислить расстояние от точки K (–3; 4; –8) до плоскости Р, проходящей через точку M 0(–1; 3; –5) перпендикулярно двум плоскостям 4 x – 2 y + 3 z – 1 = 0 и 5 x + z + 9 = 0, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
15. Вычислить расстояние от точки K (7; 2; 5) до плоскости Р, проходящей через точку M 0(3; –2; 11) параллельно двум прямым 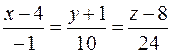 и
и 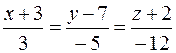 , и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
16. Вычислить расстояние от точки K (3; 1; 6) до плоскости Р, проходящей через прямую 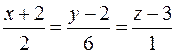 перпендикулярно плоскости –8 x + 3 y + 5 z – 1 = 0, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
перпендикулярно плоскости –8 x + 3 y + 5 z – 1 = 0, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
17. Вычислить расстояние от точки K (3; 6; –6) до плоскости Р, проходящей через две точки M 1(2; 4; –5) и M 2(2; 5; –6) параллельно вектору 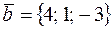 , и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
18. Вычислить расстояние от точки K (–2; –1; 7) до плоскости Р, проходящей через две параллельные прямые 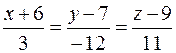 и
и 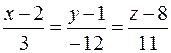 , и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
19. Вычислить расстояние от точки K (2; 1; 6) до плоскости Р, проходящей через точку M 0(–1; –4; 8) параллельно двум векторам 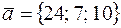 и
и 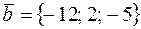 , и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
20. Вычислить расстояние от точки K (1; 3; 1) до плоскости Р, проходящей через точку M 0(5;2;–2) и прямую 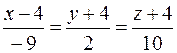 , и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
21. Вычислить расстояние от точки K (6; 3; 3) до плоскости Р, проходящей через точку M 0(4; –3; 5) параллельно вектору 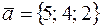 и перпендикулярно плоскости 7 x + 4 y + 3 z – 2 = 0, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
и перпендикулярно плоскости 7 x + 4 y + 3 z – 2 = 0, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
22. Вычислить расстояние от точки K (–3; 5; 3) до плоскости Р, проходящей через точку M 0(–3; 1; 2) перпендикулярно прямой 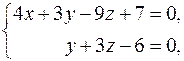 и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
23. Вычислить расстояние от точки K (1; –2; 4) до плоскости Р, проходящей через прямую 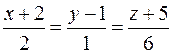 параллельно вектору
параллельно вектору 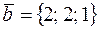 , и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
24. Вычислить расстояние от точки K (7; 2; 5) до плоскости Р, проходящей через точку M 0(2; –4; 1) перпендикулярно двум плоскостям 4 x + 3 y – 4 z + 8 = 0 и y + z – 3 = 0, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
25. Вычислить расстояние от точки K (–1; 4; –3) до плоскости Р, проходящей через точку M 0(4; –5; –2) параллельно двум прямым 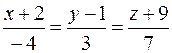 и
и 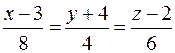 , и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
26. Вычислить расстояние от точки K (–1; –1; –9) до плоскости Р, проходящей через прямую 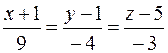 перпендикулярно плоскости 3 x + z + 4 = 0, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
перпендикулярно плоскости 3 x + z + 4 = 0, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
27. Вычислить расстояние от точки K (–6; –1; –4) до плоскости Р, проходящей через две точки M 1(–1; 2; –6) и M 2(4; –1; 2) параллельно вектору 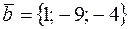 , и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
28. Вычислить расстояние от точки K (2; 3; –3) до плоскости Р, проходящей через две параллельные прямые 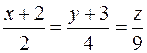 и
и 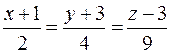 , и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
29. Вычислить расстояние от точки K (–2; 3; –1) до плоскости Р, проходящей через точку M 0(1; –2; 3) параллельно двум векторам 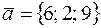 и
и  , и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
30. Вычислить расстояние от точки K (0; –1; –2) до плоскости Р, проходящей через точку M 0(3; –3; –5) и прямую 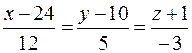 , и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
31. Вычислить расстояние от точки K (0; 2; –1) до плоскости Р, проходящей через точку M 0(–1; 1; –2) параллельно вектору 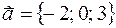 и перпендикулярно плоскости 2 x + 5 y + 6 = 0, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
и перпендикулярно плоскости 2 x + 5 y + 6 = 0, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
32. Вычислить расстояние от точки K (2; 4; 1) до плоскости Р, проходящей через точку M 0(5; 2; –4) перпендикулярно прямой 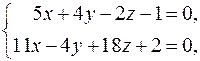 и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
33. Вычислить расстояние от точки K (4; –2; 3) до плоскости Р, проходящей через прямую 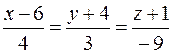 параллельно вектору
параллельно вектору 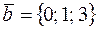 , и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
34. Вычислить расстояние от точки K (7; 2; –4) до плоскости Р, проходящей через точку M 0(2; –4; 1) перпендикулярно двум плоскостям 4 x + 3 y – 4 z + 8 = 0 и y + z – 3 = 0, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
35. Вычислить расстояние от точки K (–3; –2; –5) до плоскости Р, проходящей через точку M 0(1; 4; –3) параллельно двум прямым 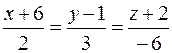 и
и 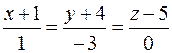 , и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
36. Вычислить расстояние от точки K (2; –4; 1) до плоскости Р, проходящей через прямую 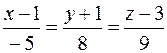 перпендикулярно плоскости 7 x – 4 y – 3 = 0, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
перпендикулярно плоскости 7 x – 4 y – 3 = 0, и записать уравнения перпендикуляра, опущенного на плоскость Р из точки K.
4. Прямая на плоскости.
1. Даны уравнения 2 х + 7 у – 4 = 0 и 4 х – 5 у + 30 = 0 двух смежных сторон параллелограмма и точка М (–6; 5) пересечения его диагоналей. Написать уравнения двух других сторон и диагоналей параллелограмма.
2. Составить уравнения сторон и вычислить координаты вершин ромба, зная одну из его вершин А (6; –1), точку O (0; 1) пересечения диагоналей и точку F (2; 3) на одной из сторон.
3. В прямоугольнике АВСD даны уравнения х + 3 у – 17 = 0 и х + 3 у + 3 = 0 двух его сторон и уравнение х + 7 у – 37 = 0 диагонали. Найти уравнения двух других сторон и второй диагонали прямоугольника.
4. Даны две С (–3; 2) и D (1; 4) смежные вершины параллелограмма АВСD и точка Q (0; –1) пересечения его диагоналей. Составить уравнения всех сторон и высоты, проведенной из вершины А к стороне ВС параллелограмма.
5. Вычислить координаты вершин и записать уравнения сторон ромба, если известны уравнения х – 7 у + 38 = 0 и х – 7 у + 8 = 0 двух его сторон и уравнение х – 2 у + 8 = 0 одной из его диагоналей.
6. Даны две вершины В (3; 7) и С (–11; –7) треугольника и точка Р (4; 3) пересечения его высот. Составить уравнения сторон и медианы, проведенной из третьей вершины треугольника.
7. В треугольнике АВС даны: уравнение стороны АВ: х + у + 1 = 0 и уравнения двух высот: АН: 3 х – 8 у + 3 = 0 и ВK: 3 х + 2 у + 9 = 0. Написать уравнение медианы, проведенной из вершины, противолежащей заданной стороне.
8. Найти координаты вершин и составить уравнения сторон треугольника, зная одну из его вершин А (1; 3) и уравнения 4 х + 7 у – 1 = 0 и х – 4 у – 13 = 0 двух высот. Записать уравнение третьей его высоты.
9. Даны уравнения х – 2 у – 4 = 0, 5 х – у + 7 = 0 и х + у – 1 = 0 двух сторон треугольника и медианы. Составить уравнения третьей стороны треугольника и его высоты, опущенной на эту сторону.
10. Составить уравнения сторон треугольника, зная одну его вершину В (–1; 5), а также уравнения высоты 3 х + у + 5 = 0 и медианы 3 х + 2 у + 4 = 0, проведенных из одной вершины.
11. Составить уравнения сторон и вычислить координаты вершин ромба, зная одну из его вершин В (2; 1), точку S (3; 3) пересечения диагоналей и точку R (1; 2) на одной из сторон (проходящих через вершину В).
12. Даны уравнения х + 3 у + 7 = 0, 3 х – 8 у + 4 = 0 и 4 х – 5 у – 6 = 0 двух сторон треугольника и медианы. Составить уравнения третьей стороны треугольника и его высоты, опущенной на эту сторону.
13. В прямоугольнике АВСD даны уравнения 4 х – у + 34 = 0 и 4 х – у – 17 = 0 двух его сторон и уравнение 7 х + 11 у – 17 = 0 диагонали. Найти уравнения двух других сторон и второй диагонали прямоугольника.
14. Даны две вершины С (–4; –4) и А (3; –3) треугольника и точка Q (–1; 5) пересечения его высот. Составить уравнения сторон и медианы, проведенной из третьей вершины треугольника.
15. Даны две D (4; 1) и А (–2; 3) смежные вершины параллелограмма АВСD и точка R (1; 0) пересечения его диагоналей. Составить уравнения всех сторон и высоты, проведенной из вершины В к стороне СD параллелограмма.
16. Найти координаты вершин и составить уравнения сторон треугольника, зная одну из его вершин В (–3; 4) и уравнения х – 5 у + 4 = 0 и 4 х – 3 у + 5 = 0 двух высот. Записать уравнение третьей его высоты.
17. Вычислить координаты вершин и записать уравнения сторон ромба, если известны уравнения 13 х – у + 28 = 0 и 13 х – у – 108 = 0 двух его сторон и уравнение 3 х + 5 у – 4 = 0 одной из его диагоналей.
18. Составить уравнения сторон треугольника, зная одну его вершину С (5; 2), а также уравнения высоты 2 х – у – 2 = 0 и медианы х – у = 0, проведенных из одной вершины.
19. Даны уравнения 2 х + у + 5 = 0 и 4 х + 7 у = 0 двух смежных сторон параллелограмма и точка М (1; –2) пересечения его диагоналей. Написать уравнения двух других сторон и диагоналей параллелограмма.
20. В треугольнике АВС даны: уравнение стороны ВС: 7 х – 2 у + 13 = 0 и уравнения двух высот: СР: 5 х + 2 у – 1 = 0 и ВR: 3 х – 5 у – 11 = 0. Написать уравнение медианы, проведенной из вершины, противолежащей заданной стороне.
21. В прямоугольнике АВСD даны уравнения х – у + 2 = 0 и х – у + 6 = 0 двух его сторон и уравнение 3 х – 7 у + 26 = 0 диагонали. Найти уравнения двух других сторон и второй диагонали прямоугольника.
22. Даны две вершины А (–10; 8) и В (11; 1) треугольника и точка Н (5; –7) пересечения его высот. Составить уравнения сторон и медианы, проведенной из третьей вершины треугольника.
23. Даны две А (2; –4) и В (4; 2) смежные вершины параллелограмма АВСD и точка O (1; –1) пересечения его диагоналей. Составить уравнения всех сторон и высоты, проведенной из вершины С к стороне АD параллелограмма.
24. Найти координаты вершин и составить уравнения сторон треугольника, зная одну и его вершин С (–2; –4) и уравнения 6 х + 5 у – 16 = 0 и х + 2 у – 6 = 0 двух высот. Записать уравнение третьей его высоты.
25. Вычислить координаты вершин и записать уравнения сторон ромба, если известны уравнения х + 4 у + 9 = 0 и х + 4 у – 21 = 0 двух его сторон и уравнение х – у – 1 = 0 одной из его диагоналей.
26. Составить уравнения сторон треугольника, зная одну его вершину А (3; –7), а также уравнения высоты 2 х + 3 у + 5 = 0 и медианы х + 3 у + 7 = 0, проведенных из одной вершины.
27. Даны уравнения 3 х – 5 у + 7 = 0 и х + 5 у + 9 = 0 двух смежных сторон параллелограмма и точка Р (1; 0) пересечения его диагоналей. Написать уравнения двух других сторон и диагоналей параллелограмма.
28. В треугольнике АВС даны: уравнение стороны АС: х – 3 у – 10 = 0 и уравнения двух высот: АQ: 3 х + у = 0 и СМ: х – 5 у – 4 = 0. Написать уравнение медианы, проведенной из вершины, противолежащей заданной стороне.
29. Составить уравнения сторон и вычислить координаты вершин ромба, зная одну из его вершин D (–4; 1), точку N ( 2; – 1) пересечения диагоналей и точку Т (–5; –1) на одной из сторон.
30. Даны уравнения х – у + 4 = 0, 2 х + 3 у – 17 = 0 и у – 3 = 0 двух сторон треугольника и медианы. Составить уравнение третьей стороны треугольника и его высоты, опущенной на эту сторону.
31. Даны две В (–3; 1) и С (1; –4) смежные вершины параллелограмма АВСD и точка Н (2; 2) пересечения его диагоналей. Составить уравнения всех сторон и высоты, проведенной из вершины D к стороне АВ параллелограмма.
32. Найти координаты вершин и составить уравнения сторон треугольника, зная одну из его вершин А (3; –3) и уравнения 7 х – 4 у + 2 = 0 и х – 7 у + 11 = 0 двух высот. Записать уравнение третьей его высоты.
33. Вычислить координаты вершин и записать уравнения сторон ромба, если известны уравнения х – 8 у + 11 = 0 и х – 8 у – 49 = 0 двух его сторон и уравнение 2 х – у – 8 = 0 одной из его диагоналей.
34. Составить уравнения сторон треугольника, зная одну его вершину В (–9; –6), а также уравнения высоты 4 х + у + 13 = 0 и медианы 2 х – у + 5 = 0, проведенных из одной вершины.
35. Даны уравнения 7 х + 4 у + 63 = 0 и 3 х + 10 у + 27 = 0 двух смежных сторон параллелограмма и точка K (–2; –5) пересечения его диагоналей. Написать уравнения двух других сторон и диагоналей параллелограмма.
36. В треугольнике АВС даны: уравнение стороны АВ: х + у + 2 = 0 и уравнения двух высот: АN: 4 х + у + 11 = 0 и ВD: 6 х – у + 5 = 0. Написать уравнение медианы, проведенной из вершины, противолежащей заданной стороне.
5. Уравнение прямой в отрезках.
Через точку С провести прямую так, чтобы площадь треугольника, образованного ею и осями координат, была равна S квадратным единицам.
| вариант | |||||||||
| С | –8; –9 | 2; –2 | 8; 3 | –4; 2 | 1; 2 | 6; 1 | –4; –5 | 9; –4 | –8; 6 |
| S, кв. ед. | 1,5 | ||||||||
| вариант | |||||||||
| С | 4; 3 | 2; –3 | 2; –9 | –3; 8 | 6; 6 | 5; –6 | –2; 2 | 4; 4 | –3; 2 |
| S, кв. ед. | 1,5 | 7,5 | 1,5 | ||||||
| вариант | |||||||||
| С | 2; 4 | –8; 1 | –6; –2 | 8; –5 | 1; –4 | 4; 6 | 4; –1 | 6; 8 | –2; –6 |
| S, кв. ед. | |||||||||
| вариант | |||||||||
| С | 8; –1 | –4; 3 | –8; –2 | 5; –4 | 6; 5 | –5; –8 | 3; 2 | 8; 3 | 4; –2 |
| S, кв. ед. | 7,5 |
6. Поворот вектора на угол.
1. Даны уравнения двух сторон квадрата: x – 3 y + 8 = 0 и x – 3 y – 2 = 0. Составить уравнения двух других его сторон при условии, что точка A (–6; –6) лежит на стороне этого квадрата.
2. Точка B (1; 4) является вершиной квадрата, диагональ которого лежит на прямой 3 x – 4 y – 12 = 0. Найти координаты остальных вершин квадрата.
3. В прямоугольном треугольнике при вершине С (4; –1) острый угол равен arctg3 и уравнение противолежащего катета 2 x + y – 2 = 0. Найти координаты остальных вершин прямоугольника.
4. Даны две противоположные вершины квадрата A (5; 1) и С (–4; 2). Найти координаты двух других вершин и составить уравнения диагоналей квадрата.
5. Из точки F (0; –4) направлен луч под углом arctg2 к прямой 2 x – y + 6 = 0. Найти уравнение луча, отраженного от этой прямой.
6. Точка С (–4; –5) является вершиной квадрата, одна из сторон которого лежит на прямой x – 2 y + 4 = 0. Найти координаты остальных вершин квадрата.
7. Найти координаты вершин прямоугольного равнобедренного треугольника, зная уравнение гипотенузы 2 x – 3 y – 5 = 0 и вершину прямого угла A (–1; 2).
8. Даны уравнения двух сторон квадрата x + 2 y – 9 = 0 и x + 2 y + 6 = 0. Составить уравнения двух других его сторон при условии, что точка F (–4; 4) лежит на стороне этого квадрата.
9. Точка С (2; 5) является вершиной квадрата, диагональ которого лежит на прямой 2 x + 3 y – 6 = 0. Найти координаты остальных вершин квадрата.
10. В прямоугольном треугольнике при вершине А (–9; 5) острый угол равен arctg5 и уравнение противолежащего катета x + 2 y + 4 = 0. Найти координаты остальных вершин прямоугольника.
11. Даны две противоположные вершины квадрата В (–3; 1) и D (3; 3). Найти координаты двух других вершин и составить уравнения диагоналей квадрата.
12. Из точки N (–8; 8) под углом arctg4 к прямой 3 x – 2 y – 12 = 0 направлен луч. Найти уравнение луча отраженного от этой прямой.
13. Точка D (–5; 1) является вершиной квадрата, одна из сторон которого лежит на прямой x + 2 y – 7 = 0. Найти координаты остальных вершин квадрата.
14. Найти координаты вершин прямоугольного равнобедренного треугольника, зная уравнение гипотенузы 2 x + 3 y = 0 и вершину прямого угла В (3; 5).
15. Даны уравнения двух сторон квадрата 4 x + y + 33 = 0 и 4 x + y – 18 = 0. Составить уравнения двух других его сторон при условии, что точка N (–1; 5) лежит на стороне этого квадрата.
16. Точка D (–8; –5) является вершиной квадрата, диагональ которого лежит на прямой 3 x + 5 y + 15 = 0. Найти координаты остальных вершин квадрата.
17. В прямоугольном треугольнике при вершине В (5; 1) острый угол равен arctg2 и уравнение противолежащего катета 2 x – y + 6 = 0. Найти координаты остальных вершин треугольника.
18. Даны две противоположные вершины квадрата С (6; 2) и А (–5; 3). Найти координаты двух других вершин и составить уравнения диагоналей квадрата.
19. Из точки Р (1; 4) направлен луч под углом 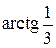 к прямой x + 3 y – 3 = 0. Найти уравнение луча, отраженного от этой прямой.
к прямой x + 3 y – 3 = 0. Найти уравнение луча, отраженного от этой прямой.
20. Точка А (2; 4) является вершиной квадрата, одна из сторон которого лежит на прямой 7 x + 5 y + 40 = 0. Найти координаты остальных вершин квадрата.
21. Найти координаты вершин прямоугольного равнобедренного треугольника, зная уравнение гипотенузы 11 x – 5 y – 13 = 0 и вершину прямого угла С (6; –4).
22. Даны уравнения двух сторон квадрата 2 x – 5 y – 45 = 0 и 2 x – 5 y + 13 = 0. Составить уравнения двух других его сторон при условии, что точка Р (3; –2) лежит на стороне этого квадрата.
23. Точка А (–1; –4) является вершиной квадрата, диагональ которого лежит
 2015-10-22
2015-10-22 4277
4277