В) додавання до якогось рядка (або стовпця) іншого рядка (або стовпця), помноженого на довільне число

Слід зауважити, що зводячи матрицю до трапецоїдного виду треба домогтися того, щоб по “головній діагоналі” були розташовані спочатку елементи, що не дорівнюють нулю (тобто 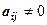при 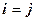), а потім нульові ( 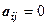при 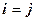, якщо вони є). Тоді ранг матриці дорівнює числу не рівних нулю елементів “головної діагоналі” (числу ненульових рядків матриці).

Вправи. Визначити ранг матриць методом окантованих мінорів:

1) А = .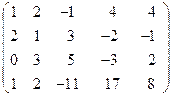

Відповідь: Rg A = 4.

2) B = .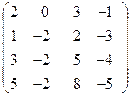

Вiдповiдь: Rg B = 2.

3) C = .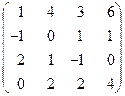

Вiдповiдь: Rg C = 3.

Критерій сумісності лінійної системи

Розглянемо систему

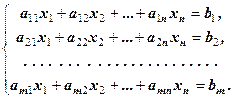(8.1)

Позначимо:

А = — матриця системи,

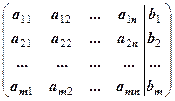= — розширена матриця системи.

Стовпці матриці А будемо позначати

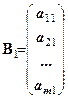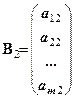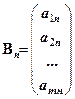, , ..., , B = .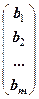

Тоді систему (8.1) можна замінити матричним рівнянням

B ₁ x ₁ + B ₂ x ₂ +... + B _n x _n = B. (8.2)