2015-10-22
1990
Розглянемо матрицю A mn. Розбиваючи її горизонтальними та вертикальними прямими на матриці (блоки, клітини) меншого порядку, одержимо так звану блочну матрицю, елементами якої будуть матриці.
Наприклад,
А 3x4 = 
Þ M 2x3 = 
,
де М 2х3 — блочна (клітинна) матриця.
Матрицю A mn можна розбити на блоки таким чином, що її елементами будуть тільки рядки або тільки стовпці первісної матриці
A mn = 
= 
,
де 
, 
, ...,
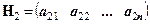А mn = = 
,
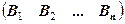де 
, 
, ..., 
.
Розглянемо нульову лінійну комбінацію складену із стовпців матриці A mn.
k1В1 + k2В2 +...+ knВn = 0 (7.1)
Або коротко: 
.
Якщо рівність (7.1) справджується за умови, що всі коефіцієнти ki = 0, то стовпці матриці A mn є лінійно незалежні; якщо ж деякі із коефіцієнтів рівності (7.1) не дорівнюють нулю, то стовпці матриці А mn є лінійно залежні.
У випадку лінійної залежності будь-який із стовпців може бути поданий як лінійна комбінація інших стовпців.
Виділимо в матриці А mn які-небудь s рядків і s стовпців (1 £ s £ min (m,n)). Тоді сукупність елементів, які знаходяться на перетині виділених рядків і стовпців, утворює квадратну матрицю s -го порядку, детермінант якої називається мінором s -го порядку даної матриці.
Наприклад, із матриці
можна скласти 9 мінорів першого порядку, 9 мінорів другого порядку, 1 мінор третього порядку:
М 1(1) = |1|, M 2(1) = |2|, M 3(1) = |0| і т.д.
М 1(2) = 
, M 2(2) = 
, M 3(2) = 
і т. д.
М (3) = 
.
Означення. Рангом матриці А називають найвищий порядок відмінного від нуля мінора цієї матриці і позначають Rg A або rang A.
Отже, ранг матриці дорівнює r, якщо існує мінор цієї матриці r -го порядку, що відмінний від нуля, а всі мінори
(r + 1)-го порядку дорівнюють нулю або не існують.
Вправи. Знайти ранг матриць:
1) А = (1 5 7).
Відповідь: Rg A = 1.
2) B = 
.
Відповідь: Rg B = 1.
3) C = 
.
Відповідь: Rg C = 2.
4) D = 
.
Відповідь: Rg D = 2.
5) E = 
.
Відповідь: Rg E = 2.
6) K =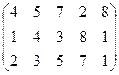 
.
Відповідь: Rg K = 3.
7) M =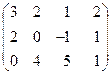 
.
Відповідь: Rg M = 2.
Зауважимо, що безпосередньо (згідно з означенням) знайти ранг матриці, як правило, важко, оскільки у деяких випадках треба обчислювати дуже багато мінорів, що утворені з даної матриці. Тому надалі ми будемо використовувати так званий метод обвідних мінорів, що випливає з теореми про базисний мінор.
Означення. Базисним мінором матриці називають відмінний від нуля її мінор, порядок якого дорівнює рангу матриці. Звичайно, такий мінор, взагалі кажучи, не єдиний.
Рядки і стовпці, на перетині яких знаходяться елементи базисного мінору, називають базисними.
Наведемо без доведення так звану теорему про базисний мінор.
Усі рядки (стовпці) базисного мінора матриці A лінійно незалежні, а будь-який інший рядок (стовпець) матриці А є лінійна комбінація рядків (стовпців) базисного мінора.
Із цієї теореми випливає метод обвідних мінорів. Суть його полягає у тому, що при знаходженні рангу матриці переходять від мінорів меншого порядку до мінорів вищого порядку; причому, якщо уже знайдено мінор r - го порядку, що відмінний від нуля, то обчислюють лише ті мінори (r + 1)-го порядку, що обводять (тобто містять у собі) цей мінор. Якщо всі вони дорівнюють нулю, то ранг матриці дорівнює r.
Метод обвідних мінорів особливо зручно застосовувати по відношенню до трапецоїдної матриці (зокрема трикутної), так як у цьому випадку дуже легко обчислити необхідні нам мінори.
Наприклад, для трикутної матрицi
А = 
очевидно, що ранг дорiвнює 4, а для трапецоїдної матриці
В = 
ранг дорівнює 3, тобто числу ненульових рядків цієї матриці.
В тому випадку, коли матриця не є трапецоїдною, то її можна звести до трапецоїдного виду, застосовуючи елементарні перетворення, які не порушують рангу матриці.
Дотаких елементарних перетворень відносять такі операції:
а) множення рядка (або стовпця) на довільне дійсне число, яке відмінне від нуля;
б) переставлення (транспозиція) двох рядків (або стовпців);
