Поняття рангу та базисного мінору матриці

Розв’язування матричних рівнянь

За допомогою оберненої матриці

Розв’язування квадратних

Матричних рівнянь

Розглянемо матричні рівняння 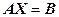або 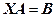, де матриц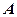і і 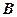— квадратні однакового порядку 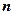, крім того матриця 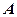має обернену матрицю. Тоді ці рівняння можна розв’язати шляхом множення зліва (справа) обох частин рівняння на матрицю 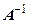. Отримаємо

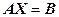
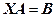
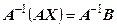
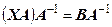
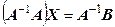
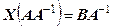
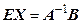
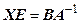
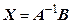
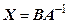
Вправи. Розв’язати системи:

1) 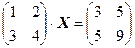. Відповідь: .

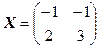2) 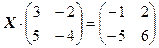. Відповідь: .

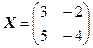3) 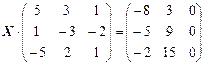. Відповідь: .

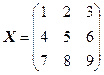Розв’язування квадратних

Лінійних систем

Розглянемо матричне рівняння AX = B, що відповідає квадратній лінійній системі рівнянь

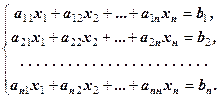(6.1)

А = 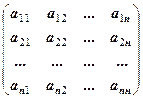— матриця системи, detA ¹ 0,

X = 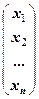— матриця невідомих,

B = 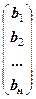— матриця вільних членів.

Для знаходження матриці Х використаємо формулу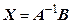

Вправи. Розв’язати системи:

1) 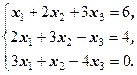Відповідь: Х =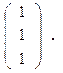

2) 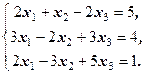Відповідь: Х =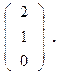

3) 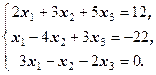Відповідь: Х = .

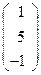Поняття рангу та базисного мінору матриці.