Системы трех линейных уравнений и определители третьего порядка

Рассмотрим систему трех линейных уравнений с тремя неизвестными:

Определитель, составленный из коэффициентов при неизвестных, называется определителем системы или главным определителем:

.

Если то система имеет единственное решение, которое определяется по формулам Крамера:

где

где определители – называются вспомогательными и получаются из определителя путем замены его первого, второго или третьего столбца столбцом свободных членов системы.

Пример 2. Решить систему .

Сформируем главный и вспомогательные определители:

Осталось рассмотреть правила вычисления определителей третьего порядка. Их три: правило дописывания столбцов, правило Саррюса, правило разложения.

а) Правило дописывания первых двух столбцов к основному определителю:

.

Вычисление проводятся следующим образом: со своим знаком идут произведения элементов главной диагонали и по параллелям к ней, с обратным знаком берут произведения элементов побочной диагонали и по параллелям к ней.

б) Правило Саррюса:

Со своим знаком берут произведения элементов главной диагонали и по параллелям к ней, причем недостающий третий элемент берут из противоположного угла. С обратным знаком берут произведения элементов побочной диагонали и по параллелям к ней, третий элемент берут из противоположного угла.

в) Правило разложения по элементам строки или столбца:

Если , тогда .

Алгебраическое дополнение – это определитель более низкого порядка, получаемый путем вычеркивания соответствующей строки и столбца и учитывающий знак , где 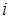– номер строки, – номер столбца.

Например,

, , и т.д.

Вычислим по этому правилу вспомогательные определители и , раскрывая их по элементам первой строки.

Вычислив все определители, по правилу Крамера найдем переменные:

Проверка:

Вывод: система решена верно: .