Диметрическая проекция — это аксонометрическая проекция, у которой коэффициенты искажения по двум осям имеют равные значения, а искажение по третьей оси может принимать иное значение.
Положение аксонометрических осей для прямоугольной диметрии показано на рис. 9.6,а. Коэффициенты искажения, определяемые из пространственной модели, равны: по оси Y’ — 0,47, а по осям X’ и Z’ — 0,94. Для упрощения построений ГОСТ 2.317-69 предлагает взять kx = kz = 1, a ky = 0,5, т.е. и в прямоугольной диметрии изображение предмета будет немного уваливаться.
Практически способ построения аксонометрических осей в прямоугольной диметрии показан на рис. 9.6,б. Через точку 0’ проводим вспомогательную прямую, перпендикулярную к выбранной вертикальной оси Z’. В обе стороны от точки 0’ откладываем на этой прямой по 8 произвольных, но равных между собой отрезков. В направлении отрицательной градуировки оси Z’ от левой конечной точки откладываем один такой же отрезок, а от правой конечной точки — 7 отрезков. Соединив полученные точки с точкой 0’ прямыми линиями, получим направления аксонометрических осей, подобные показанным на рис. 9.6,а.

Если направление проецирования не перпендикулярно к аксонометрической плоскости проекций, то аксонометрия называется косоугольной. В этом виде аксонометрии одна из координатных плоскостей, расположена параллельно картинной плоскости, поэтому все геометрические фигуры, расположенные в такой плоскости, проецируются на картину без искажения. В связи с этим косоугольную аксонометрию удобно применять в тех случаях, когда изображаемый объект (деталь) содержит большое число окружностей, находящихся в координатной плоскости, располагаемой параллельно картинной плоскости.
Если координатная плоскость XOZ параллельна аксонометрической плоскости, то такая косоугольная аксонометрия называется фронтальной.
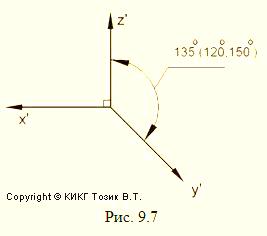
В этом случае оси OX и OZ проецируются без искажения, т.е. kx = kz = 1, a ∠X’O’Z’ = 90°. ГОСТ 2.317-69 допускает два вида косоугольных фронтальных аксонометрии (рис. 9.7)
1) косоугольную фронтальную изометрию, когда kx = ky = kz = 1, а ∠Y’O’Z’ = 135° (допускаются 120° или 150°)
2) косоугольную фронтальную диметрию, когда kx = kz = 1, ky = 0,5, а ∠Y’O’Z’ = 135° (допускаются 120° или 150°).
Показатели искажения по осям, kx = kz = 1, ky = 0,5. ГОСТ 2.317–69 допускает применять косоугольную диметрию с углом наклона оси 01y1, равным 30° и 60°.
 2015-10-22
2015-10-22 2314
2314








