Рассмотрим первое начало термодинамики с точки зрения статистической физики. Как известно  , откуда
, откуда
 . (2.33)
. (2.33)
Внутренняя энергия находится по правилу нахождения средних от гамильтониана:
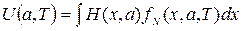 , (2.34)
, (2.34)
где a – внешний параметр.
Возьмём дифференциал по а и Т от (2.34)
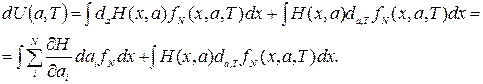 (2.35)
(2.35)
Теперь рассмотрим микроскопические силы. Они определяются выражением  а макроскопическая сила находится по правилу средних от микроскопических сил:
а макроскопическая сила находится по правилу средних от микроскопических сил:  т.е. работа макроскопических сил
т.е. работа макроскопических сил  . Сравнивая это выражение с (2.35) и (2.33), можно прийти к выводу, что
. Сравнивая это выражение с (2.35) и (2.33), можно прийти к выводу, что
 . (2.36)
. (2.36)
Умножим и разделим (2.36) на kT и вспомним каноническое распределение Гиббса:
 ,
,
и представим его в виде:
 , (2.37)
, (2.37)
т.е.  (2.37а)
(2.37а)
Из условия нормировки  возьмём дифференциал по а и Т
возьмём дифференциал по а и Т
 . (2.38)
. (2.38)
Учитывая это, представим (2.36) в виде
 . (2.39)
. (2.39)
Или, учитывая (2.37)
 . (2.40)
. (2.40)
Количество теплоты в свою очередь можно представить, как  , откуда энтропия равна
, откуда энтропия равна
 . (2.41)
. (2.41)
И, в заключение, несколько слов о величине F (a, T). Рассмотрим формулу для свободной энергии, полученную ранее  . Подставим в эту формулу (2.41) и (2.34)
. Подставим в эту формулу (2.41) и (2.34)
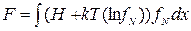 . (2.42)
. (2.42)
Сравнив (2.42) и (2.37), получим
 , (2.43)
, (2.43)
откуда следует, что введённая нами в (2.37) величина имеет смысл свободной энергии.
Для дискретного случая энтропию можно представить в виде
 ,
,
где pi – вероятность i -го микросостояния системы. Легко показать, что распределение вероятностей, когда одно из значений pi равно единице, а остальные нулю, приводит к минимальному значению энтропии, равному нулю.
С другой стороны, максимально значение энтропии соответствует равновероятному распределению. В этом случае энтропия равна
 ,
,
где Ω – число микросостояний (ранее введенная величина – статистический вес). Таким образом, энтропия может выступать в качестве меры беспорядка системы.
 2015-10-22
2015-10-22 864
864








