Связь квантовых и классических распределений Гиббса

Чтобы от квантовых распределений перейти к классическим функциям, надо перейти от суммирования к интегрированию . Для этого выделим в фазовом пространстве (пространстве координат-импульсов всех частиц) элементарную ячейку (а в классической механике можно сделать объём сколь угодно малым). Объём этой ячейки, учитывая соотношение неопределённостей Гейзенберга, (Δ x Δ p_x ≤ h ³, V =Δ x Δ p_x). h ^{3 N} – объём всех частиц.

Для перехода от к нужно вместо интегрирования по всему фазовому пространству провести интегрирование лишь по тем областям, которые соответствуют различным физическим состояниям. Для N частиц таких состояний будет в N! раз меньше (как следствие тождественности одинаковых частиц), т.е. интеграл будет выглядеть так:

.

Парадокс Гиббса

Представим себе мысленный эксперимент: пусть имеется сосуд, который наполнен газом и разделён на два одинаковых отсека перегородкой (рис.2.9). Свойства газа в отсеках абсолютно одинаковы. Если убрать перегородку, то из физических соображений ничего не должно произойти, т.е. энтропия системы должна остаться неизменной. Посчитаем её. Энтропия до убирания перегородки:

. (2.46)

Уберём перегородку: 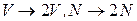. Изменяется и значение энтропии:

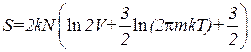, (2.47)

, (2.48)

т.е. энтропия возрастает, хотя не должна. Ответ на это противоречие заключается в том, что энтропия определена с точностью до константы (). Гиббс предложил следующее выражение для S ₀:

. (2.49)

Но, если использовать квантовое распределение Гиббса – парадокса можно избежать. Здесь выражение для S ₀ выглядит по-другому:

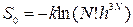, (2.50)

, т.е. если , то формула совпадает с (2.49).

2.10. Третье начало термодинамики с точки зрения статистической
физики

Одним из основных положений термодинамики является утверждение о том, что энтропия всякого тела стремится к нулю при стремлении к нулю температуры:

. (2.51)

Это утверждение представляет собой содержание так называемой теоремы Нернста. Иногда утверждение (2.51) называют третьим началом термодинамики.

С точки зрения статистической физики это утверждение может быть интерпретировано следующим образом. Рассмотрим систему, находящуюся в равновесии при температуре, стремящейся к нулю кельвинов. При этом система находится в состоянии с наименьшей энергией (основном состоянии). Тогда в каноническом распределении Гиббса наибольшим будет слагаемое, отвечающее наименьшей энергии, а остальные будут стремиться к нулю (в силу условия нормировки). Как было показано ранее, такое распределение соответствует энтропии системы и равно нулю. Таким образом, третье начало термодинамики с точки зрения статистической физики можно сформулировать так: при нуле кельвинов система находится, в основном, в полностью определенном состоянии, что соответствует нулевой энтропии (как мере неопределенности).

Флуктуации

Пусть ƒ — любая физическая величина, испытывающая флуктуации. Флуктуацией величины ƒ называется отклонение мгновенного значения этой величины от ее среднего значения. Очевидно, что <Δƒ> = 0. Поэтому обычно пользуются средним квадратом флуктуации, т.е. величи­ной (<Δƒ>)². Квадратный корень из этой величины называется — среднеквадратичной относительной флуктуацией.

Усредняя выражение , получим

.

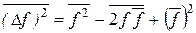Но ƒ – величина постоянная, а потому 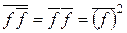. Следовательно,

. (2.52)

Усредним теперь произведение двух флуктуирующих величин:

fg = (< f> + Δƒ) (< g> + Δ g)= ,

Так как f и g — величины постоянные, а (<Δƒ>)= <Δ g >= 0, то

. (2.53)

Формула (2.52) содержится здесь как частный случай, который получает­ся при g = f.

Величины f и g называются статистически независимыми, если

<Δ f Δ g >= 0.

Для таких величин:

<fg>=<f><g>. (2.54)

Рассмотрим теперь любую физическую систему, состоящую из N независимых одинаковых частей. Примером такой системы может служить идеальный газ, а составных частей — отдельные молекулы. Пусть f_t — произвольная аддитивная величина, характеризующая i -ю подсистему, например, в приведенном примере - кинетическая энергия r '-й молекулы. Тогда в силу предполагаемой аддитивности соответствующая величина для всей системы будет F = Σ ƒ_i. Выразим средний квадрат флуктуации вели­чины F через аналогичный квадрат для величины ƒ_i. Очевидно, < F> = Σ <ƒ>_i = N<f>, где индекс i опущен, так как предполагается, что все составные части системы тождественны. Далее,

.

А так как эти части независимы, то <ƒ_i ƒ_j >= <ƒ_i >< ƒ_j >=(<ƒ>)². Следовательно, .

Подставляя эти значения в формулу (2.52), получим

. (2.55)

Отсюда на основании (2.52)

. (2.56)

С увеличением N относительная флуктуация величины F убывает обратно пропорционально При больших N относительные флуктуации ничтожны. Этот вывод качественно верен и для неаддитивных величин. С ним связана достоверность термодинамических результатов для больших макроскопических систем.

В соответствии со сказанным видим, что в объемах с большим средним числом частиц N относительные флуктуации малы и трудно доступны наблюдению. Наоборот, при малых N относительные флуктуации велики. Более общий метод вычисления флуктуации плотности, применимый также к жидкостям и твердым телам, основан на теореме о равномерном распределении кинетической энергии по степеням свободы. Рассмотрим малую часть жидкости или газа, окруженную такой же жидкой или газооб­разной средой, температура Т которой поддерживается постоянной (тер­мостатом). С целью упрощения и наглядности вычислений предположим, что малая часть жидкости или газа заключена в цилиндр с поршнем. Стенки цилиндра идеально проводят тепло, а поршень может ходить в нем без трения. Тогда наличие стенок цилиндра и поршня не будет препятствовать обмену энергией и выравниванию давлений между веществом в цилиндре и термостатом. Тепловое движение молекул вещества вызовет броуновское движение поршня. К этому движению поршня мы и применим теорему о равномерном распределении кинетической энергии по степеням свободы. Поршень можно рассматривать как гармонический осциллятор, совер­шающий беспорядочные тепловые колебания. Среднее значение его потен­циальной энергии при смещении на х из положения равновесия х = 0 равно (1/2)к х² = ( 1/2 )кТ, где к — жесткость, соответствующая такому смеще­нию. Если S — площадь поршня, a AV — изменение объема системы, то D V = Sx. Таким образом, < ( Δ V)² > = < S²x²>= S²kT/K. Сила, возвращающая поршень в положение равновесия, будет , где Р — давление газа или жидкости. Поэтому к = — SdP/dх =S²dP/dV. В результате получим

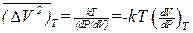. (2.57)

Знак Т указывает, что в выводе предполагалось постоянство температуры окружающей среды (термостата). Если бы вещество внутри объема V было адиабатически изолировано, то индекс Т следовало бы заменить на S (постоянство энтропии), т.е.

<(Δ V ² )>_s = - kT(dV/dP)_s. (2.58)

Формулы (2.57) и (2.58) выражают флуктуации объема одной и той же массы вещества, находящейся в термодинамическом равновесии с окружающей средой.

Для идеального газа при постоянной температуре PV = const, так что (dV/dP) _т = -V/P. А так как PV - NкТ, где N - число молекул в объеме V, то из формулы (2.57) получаем (Δ V ² )=V²/N.

Перейдем теперь к вычислению флуктуации энергии. С целью лучшего уяснения метода начнем с вычисления флуктуации кинетической энергии e молекулы одноатомного идеального газа в отсутствие силовых полей. Согласно максвелловскому закону распределения скоростей

, (2.59)

где α = 1/кT, dГ - элементы объема пространства скоростей, а Z определяется условием нормировки:

. (2.60)

Дифференцируя это соотношение по параметру α, получим

и формула (2.59) перейдет в

. (2.61)

Отсюда

.

Аналогично

. (2.62)