Распределение Максвелла

Распределения Гиббса, будучи строгими для макроскопических систем, тем не менее не удобны для вычисления средних значений ввиду их сложности (в них используется полная энергия системы частиц, которая зависит от координат и импульсов всех частиц). Поэтому существует необходимость в нахождении более простых функций распределения. Такой функцией распределения является распределение молекул по скоростям, полученное Максвеллом. Максвелл получил свое распределение молекул газа по скоростям раньше, чем были записаны распределения Гиббса.Формула Максвелла была во многом интуитивной, хотя впоследствии была не только строго выведена из канонического распределения Гиббса, но и подтверждена экспериментально.

Максвелл предположил, что вероятность того, что скорости частицы в равновесном идеальном газе находятся в интервале (dv_xdv_ydv_z), может быть записана в виде:

, (2.8)

где C – константа, которую можно найти из условия нормировки:

. (2.9)

Интеграл (3.2) можно разбить на произведение трех независимых интегралов по каждой компоненте скорости, каждый из которых является интегралом Пуассона:

. (2.10)

Тогда получим функцию распределения Максвелла по компонентам скорости:

. (2.11)

Эта функция распределения распадается на произведение трех функций распределения по каждой из компонент скорости. Например, для
x -компоненты получим

. (2.12)

Заметим, что функция распределения по компоненте скорости является симметричной относительно замены x на –x. Отсюда следует вывод о том, что среднее значение компоненты скорости x равно нулю (это можно так же подтвердить прямым взятием интеграла). Поскольку все компоненты скорости равноправны, то отсюда следует, что и средней вектор скорости равен нулю

.

Это равенство верно только в условиях равновесия.

Заметим, что в уравнении (2.9) интегрирование ведется от - ¥ до + ¥, хотя очевидно, что для любой системы с конечным числом частиц скорость каждой частицы ограничена, кроме того, она не может быть больше скорости света.

Найдем теперь распределение Максвелла по модулю скорости. Для этого нужно перейти от компонент скорости к ее модулю по формуле

,

а также определить физически бесконечно малый объем в пространстве модулей скорости. Такой объем соответствует объему тонкой сферы радиуса v и равен 4π v²v. Проводя соответствующие замены переменных, получим функцию распределения Максвелла по модулю скорости:

. (2.13)

Нетрудно убедиться, что функция распределения является нормированной.

Исследуем свойства функции распределения по модулю скорости.

Во-первых, беря производную от функции F(v), и приравнивая ее к нулю, можно найти максимум функции распределения, который соответствует наиболее вероятной скорости частиц:

.

Два других экстремума v = 0 и v = ∞ являются минимумами функции распределения.

Найдем среднее значение модуля скорости. По правилу нахождения средних получим

. (2.14)

Занося одну из скоростей под дифференциал, получим интеграл, который можно взять по частям. В результате получим:

. (2.15)

Найдем так же средний квадрат скорости:

(2.16)

Этот интеграл является табличным, и может быть легко получен из интеграла Пуассона

.

Полученная величина позволяет найти среднее значение кинетической энергии молекул

.

Этот результат без вывода был получен в элементарной кинетической теории.

Вид распределения Максвелла для молекул азота показан
на рис. 2.3. Температуры на рисунке равны: T₁ = 50 К, T ₂ = 100 К,
T₃ = 300 К. С увеличением скорости максимум распределения смещается в сторону больших скоростей, а высота кривой в максимуме несколько понижается. Наличие максимума объясняется тем, что кривая отражает результат двух противоборствующих тенденций: вероятность состояний с ростом скорости падает, а плотность состояний увеличивается. При малых скоростях преобладает тенденция роста плотности состояний. При скоростях после максимума кривой преобладает тенденция уменьшения вероятности состояний.

При комнатной температуре характерные скорости молекул кислорода и азота в воздухе равны примерно 400-500 м/с. Скорости молекул водорода при этом примерно в четыре раза больше. С повышением температуры скорости молекул растут как

Частота ударов молекулы о стенку. Направим ось перпендикулярно стенке (рис. 2.4) и обозначим концентрацию молекул. Тогда плотность потока молекул в направлении стенки со скоростями между и равна

, (2.17)

где – составляющая скорости в направлении положительных значений оси (молекулы, скорости которых направлены от стенки, в образовании потока не участвуют). Тогда частота ударов молекул о стенки сосуда, приходящаяся на единицу площади, равна

(2.18)

Принимая во внимание формулу (2.15), окончательно напишем

. (2.19)

Число молекул в различных участках распределения Максвелла. Если плотность молекул , то число молекул, скорости которых распределены между и , равно

(2.20)

При вычислении (2.18) учтено, что в можно представить как 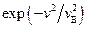, что более наглядно при анализе формы кривой распределения Максвелла. Имеются таблицы интеграла

. (2.21)

С их помощью величина (2.20) вычисляется по следующей очевидной формуле:

(2.22)

Из таблицы, в частности, находим:

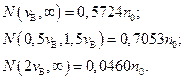
Таким образом, большая часть всех молекул имеет скорости в сравнительно небольшом интервале около наивероятнейшей, а молекул со значительными по сравнению с наивероятнейшими скоростями очень мало.

Пример 2.1. Найти число молекул кислорода О₂, скорости которых заключены в пределах от 195 до 205 м/с при . Масса кислорода 0,1 кг.

Поскольку интервал скоростей от 195 до 205 м/с достаточно мал, можно воспользоваться теоремой о среднем и по формуле (2.13) написать:

(2.23)

где м/с, м/с.

Относительная молекулярная масса кислорода и, следовательно, масса молекулы кг кг. Молярная масса кислорода кг/моль, поэтому в 0,1 кг кислорода имеется 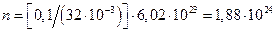молекул. Далее учтем, что Дж Дж, поэтому

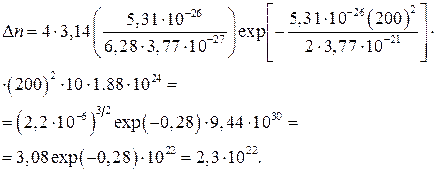
Экспериментальная проверка распределения Максвелла. Ввиду принципиальной важности распределения Максвелла для статической физики оно было много раз подвергнуто тщательной экспериментальной проверке. Принципиальная схема наиболее типичной экспериментальной установки состоит в следующем. Через отверстие выходит пучок исследуемых молекул. Чтобы в процессе движения пучка распределение молекул в нем не изменялось, они должны двигаться практически без взаимодействия друг с другом. Поэтому на пути движения пучка создается высокий вакуум, а в сосуде газ находится под низким давлением. Для того чтобы в выходящем из сосуда пучке молекулы имели такое же распределение скоростей, как в сосуде, необходимо обеспечить истечение газа через отверстие без гидродинамического напора. Это возможно, если в области вблизи отверстия молекулы не успевают сталкиваться друг с другом. Тогда молекула, попадающая в отверстие, вылетает из сосуда, не возмущая состояния всех остальных молекул в сосуде. В результате число молекул в сосуде медленно уменьшается, но их равновесное состояние не изменяется. Чтобы обеспечить такое «бесстолкновительное» покидание сосуда молекулами, отверстие по размерам должно быть много меньше длины свободного пробега молекул, т.е. среднего расстояния между последовательными столкновениями.

Для ориентировки в порядке величин полезно иметь в виду, что при нормальных условиях в воздухе молекулы сталкиваются с частотой примерно 1 млрд. в секунду, а средняя длина свободного пробега имеет порядок м. При понижении давления длина свободного пробега увеличивается. Поэтому диаметр отверстия должен быть очень малым. В эксперименте с молекулярными пучками он составляет сотые доли миллиметра. Плотность потока молекул в направлении движения пучка дается выражением (2.18).

После выхода из отверстия пучок проходит коллиматор из последовательных щелей, который выделяет движущиеся почти параллельно молекулы. Далее имеется устройство для сортировки молекул по скоростям и детектор для регистрации молекул после их сортировки.

Для сортировки молекул наиболее часто используют метод вращающихся дисков с щелями вдоль радиуса (рис. 2.5, а). С помощью этого метода Физо в прошлом столетии измерял скорость света в земных условиях. Если щели повернуты на угол друг относительно друга, а диски располагаются на расстоянии друг от друга, то при угловой скорости диски повернутся на угол в течение времени и (где ), соответствующем нескольким поворотам дисков за время прохождения молекулами расстояния . Регистрация молекул производится различными методами в зависимости от их свойств. В простейшем случае они осаждаются на экран и по толщине осажденного слоя можно судить об их числе. Так поступают, например, когда в качестве объекта исследования берется пучок атомов серебра, газ из которых образуется при нагревании в результате испарения.

В другом способе (рис. 2.5, б) селектор и детектор совмещены во вращающемся цилиндре с щелью. Когда щель попадает на линию пучка, через нее внутрь цилиндра входит порция молекул. Молекулы с различными скоростями достигают противоположной стенки цилиндра с различным запаздыванием по отношению к моменту прохождения щели и поэтому попадают на разные участки внутренней стенки цилиндра. Измеряя число молекул, попавших на различные участки, можно вычислить распределение молекул в пучке по скоростям.

В одном из очень изящных экспериментов в качестве селектора молекул использовалась сила тяжести, более медленные молекулы, падая в поле тяжести, отклоняются в направлении к земле на большее расстояние, чем быстрые молекулы. Нетрудно рассчитать отклонение в зависимости от скорости. Эти отклонения в практически осуществленном эксперименте такого рада были порядка десятых долей миллиметра, но измерения удалось надежно выполнить.

Проведенные эксперименты подтвердили справедливость распределения Максвелла.

Принцип детального равновесия. Распределение Максвелла характерно для равновесного и, следовательно, также стационарного состояния, не изменяющегося со временем. Это означает, что число частиц в каждом элементе объема вблизи скорости v пространства скоростей не изменяется с течением времени. Однако между молекулами происходят столкновения, в результате которых состав молекул в каждом элементе объема беспрерывно меняется, хотя их среднее число остается постоянным. Поэтому в единицу времени в каждый элемент объема в пространстве приходит столько же новых частиц, сколько его покидает. Спрашивается: в какие элементы объема уходят частицы и из каких приходят? Теоретически можно представить себе различные возможности, с помощью которых условия постоянства частиц во всех элементах объема будут соблюдаться.

Возьмем, например, некоторые четыре элемента объема 1–4 (см. рис. 2.6, а) и представим себе обмен частицами между ними. Каждая из стрелок изображает определенное число частиц, которые покидают рассматриваемый объем или проходят в него в единицу времени. Например, на диаграмме б (рис. 2.6) из объема 1 частицы уходят в объем 2, но такое же количество приходит в него из объема 4 и т.д. На диаграмме в (рис. 2.6) в объем 3 приходят частицы из объемов 2 и 4, но зато равное их сумме число частиц уходит в объем 1. В результате осуществления указанных обменов частицами обеспечивается постоянство частиц во всех объемах.

Однако равновесное состояние по таким схемам не может быть осуществлено. Принцип детального равновесия утверждает, что равновесие устанавливается детально, т.е. между всеми парами элементов объема. Это означает, что каждый элемент объема в единицу времени отдает в любой другой элемент объема столько частиц, сколько из него получает. Поэтому единственно возможной схемой обмена частицами между четырьмя элементами объема является схема, изображенная на рис. 2.6. Интенсивность обмена между каждой парой элементов объема, вообще говоря, различна.

Справедливость принципа детального равновесия обусловлена тем, что состояние равновесия устанавливается в результате хаотичного характера столкновения и беспорядочности движения молекул. Невозможность схем, изображенных на рис. 2.6, следует из того, что они могут быть реализованы лишь в результате определенной упорядоченности движения молекул и их столкновений. Принцип детального равновесия справедлив не только для столкновений. Он справедлив также и для всех других процессов в любых системах, равновесное состояние которых устанавливается в результате полной хаотичности процессов.