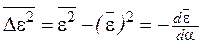Сравнение этой формулы с предыдущей дает

.

Или после подстановки параметра α = 1/кТ

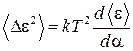. (2.63)

Так как для идеального одноатомного газа e= (3/2) кТ, то в этом случае

. (2.64)

Приведенный метод вычисления <Δε²> может быть распространен прак­тически без изменений на случай величин внешнего силового поля. На­до только максвелловское распределение заменить распределением Больцмана и производить интегрирование не только по скоростям, но и по координатам обычного пространства. В результате снова получится фор­мула (2.63), в которой, однако, под ε следует понимать уже полную энергию молекулы, состоящую из кинетической и потенциальной.

Важно отметить расширение области применимости формулы (2.63) для флуктуации полной энергии ε. Выделим малую часть (подсистему) изотропной среды (жидкости или газа), находящуюся в статистическом равновесии со всей средой, температура Т которой поддерживается по­стоянной. Подсистемой может быть и отдельная молекула. По отноше­нию к выделенной подсистеме окружающая среда играет роль термостата. Из-за обмена энергией между термостатом и подсистемой энергия последней будет непрерывно флуктуировать. Флуктуации полной энергии ε подсистемы определяются уравнением (2.63). Не имеет значения, ме­няется ли энергия ε непрерывно (классическая система), или принимает дискретный ряд значений (квантовая система). Доказательство этого утверждения дается в статистической физике. Оно основано на канони­ческом распределении Гиббса, частными случаями которого являются распределения Максвелла и Больцмана.

В случае макроскопической подсистемы, объем которой поддерживает­ся постоянным, e имеет смысл внутренней - энергии подсистемы, a d ε /dT -ее теплоемкости С_ν при постоянном объеме. Тогда из формулы(2.63) получается

<( Δε² )>_V = kT ²C_v. (2.65)

Знак V снова указывает на то, что (Δε²)_V есть средний квадрат флуктуа­ции энергии подсистемы при сохранении ее объема V постоянным.

Рассмотрим теперь флуктуации энтальпии H подсистемы. Для этого воспользуемся следующим искусственным приемом. Предположим, что подсистема заключена в оболочку с идеально проводящими подвижными стенками, так что объем подсистемы не сохраняется постоянным. Пусть оболочка снаружи подвергается действию постоянных внешних сил, под­держивающих внешнее давление Р постоянным. Эти силы увеличивают
потенциальную энергию подсистемы на величину PV. Если под e пони­мать ту же энергию, что и в предыдущем выводе, то с учетом дополнитель­ной потенциальной энергии PV среднее значение полной энергии подсисте­мы будет 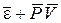.Но это есть энтальпия подсистемы H. Все предыдущие рассуждения можно повторить без изменений, заменив e на e + PV. В ре­зультате
вместо (2.63) получится

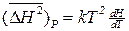. (2.56)

Но при Р = const производная dH/dT есть теплоемкость Ср подсистемы при постоянном давлении, а потому

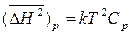. (2.67)

Изложенный метод вычисления флуктуаций можно распространить на любые величины, характеризующие макроско­пические свойства подсистем.