1. Двойственность.
Определение. Функция  называется двойственной к функции
называется двойственной к функции  , если
, если  .
.
Если взять отрицание обеих частей равенства и подставить  вместо переменных
вместо переменных 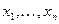 , то получится
, то получится  . Это означает, что функция
. Это означает, что функция 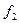 двойственна к функции
двойственна к функции 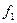 , и, таким образом, отношение двойственности является симметричным. Из определения двойственности ясно, что для любой функции двойственная ей функция определяется однозначно. В частности, может оказаться, что функция двойственна самой себе. В этом случае она называется самодвойственной.
, и, таким образом, отношение двойственности является симметричным. Из определения двойственности ясно, что для любой функции двойственная ей функция определяется однозначно. В частности, может оказаться, что функция двойственна самой себе. В этом случае она называется самодвойственной.
Пример 1. Если рассматривать логические функции, то, очевидно, дизъюнкция двойственна конъюнкции и наоборот (непосредственно следует из правил Де Моргана). Отрицание является самодвойственной функцией. Функция-константа  двойственна функции
двойственна функции  . Ещё один традиционный пример самодвойственной функции – функция
. Ещё один традиционный пример самодвойственной функции – функция  .
.
Пользуясь определением двойственности нетрудно доказать следующее утверждение, называемое принципом двойственности.
Теорема 10.1. Если в формуле  , представляющей функцию
, представляющей функцию  , все знаки функций заменить соответственно на знаки двойственных им функций, то полученная формула
, все знаки функций заменить соответственно на знаки двойственных им функций, то полученная формула  будет представлять функцию
будет представлять функцию  , двойственную функции
, двойственную функции  .
.
В булевой алгебре принцип двойственности имеет более конкретный вид, вытекающий из ранее приведённых примеров: если в формуле  , представляющей функцию
, представляющей функцию  , все конъюнкции заменить дизъюнкциями и наоборот, все единицы заменить нулями и наоборот, то получим формулу
, все конъюнкции заменить дизъюнкциями и наоборот, все единицы заменить нулями и наоборот, то получим формулу  , представляющую функцию
, представляющую функцию  , двойственную функции
, двойственную функции  .
.
Если функции равны, то двойственные им функции также равны. Это позволяет с помощью принципа двойственности получать новые эквивалентные соотношения, переходя от равенства 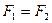 с помощью указанных замен к равенству
с помощью указанных замен к равенству  . Примером могут служить соотношения
. Примером могут служить соотношения 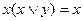 и
и 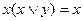 , которые могут быть получены друг из друга по указанному принципу.
, которые могут быть получены друг из друга по указанному принципу.
2. Булева алгебра и теория множеств.
Ранее были описаны булевы алгебры множеств, то есть алгебры вида  , где
, где  - булеан множества
- булеан множества  , то есть множество всех его подмножеств. Общий термин “булева алгебра” для алгебр множеств и логических функций не является случайным.
, то есть множество всех его подмножеств. Общий термин “булева алгебра” для алгебр множеств и логических функций не является случайным.
Определение. Всякая алгебра типа  называется булевой алгеброй, если её операции удовлетворяют соотношениям 1 – 10 (см. предыдущую лекцию).
называется булевой алгеброй, если её операции удовлетворяют соотношениям 1 – 10 (см. предыдущую лекцию).
В алгебре множеств элементами являются подмножества фиксированного универсального множества  . В этой алгебре операция пересечения соответствует конъюнкции, операция объединения соответствует дизъюнкции, а операция дополнения соответствует отрицанию. Само множество
. В этой алгебре операция пересечения соответствует конъюнкции, операция объединения соответствует дизъюнкции, а операция дополнения соответствует отрицанию. Само множество  является единицей, а пустое множество – нулём. Справедливость соотношений 1 – 10 для этой алгебры можно доказать непосредственно, рассматривая в них переменные как множества, а знаки логических функций – как соответствующие операции над множествами.
является единицей, а пустое множество – нулём. Справедливость соотношений 1 – 10 для этой алгебры можно доказать непосредственно, рассматривая в них переменные как множества, а знаки логических функций – как соответствующие операции над множествами.
В одной из предыдущих лекций отмечалось взаимно однозначное соответствие между множеством  , где
, где  и множеством
и множеством  двоичных векторов длины
двоичных векторов длины 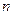 . Каждому подмножеству
. Каждому подмножеству  соответствует двоичный вектор
соответствует двоичный вектор  , где
, где 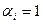 , если
, если  , и
, и  , если
, если  . Операции над векторами в булевой алгебре
. Операции над векторами в булевой алгебре  определяются следующим образом.
определяются следующим образом.
Пусть даны два вектора  и
и  из множества
из множества  . Тогда:
. Тогда:
 ,
,
 ,
,
 .
.
Поскольку компоненты (координаты) векторов принимают значения 0 или 1, то указанные операции – это просто логические операции над двоичными переменными, поэтому операции над векторами естественно назвать покомпонентными логическими операциями над двоичными векторами.
Пример 2. Даны векторы  и
и  . Найти
. Найти  .
.
Решение:
 .
.
Заметим, что подобные операции (наряду с логическими операциями над переменными) входят в систему команд любой современной ЭВМ.
Теорема 10.2. Если мощность множества  равна
равна 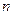
 , то булева алгебра
, то булева алгебра  изоморфна булевой алгебре
изоморфна булевой алгебре  .
.
Эта простая по содержанию теорема имеет огромное значение в математике. Она позволяет заменить теоретико-множественные операции над системой подмножеств данного множества поразрядными логическими операциями над двоичными векторами.
Похожая по формулировке, но значительно отличающаяся по смыслу теорема существует для множества всех логических функций 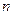 переменных
переменных 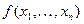 . Обозначим это множество
. Обозначим это множество 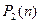 . Оно замкнуто относительно операций
. Оно замкнуто относительно операций  и, следовательно, образует конечную булеву алгебру
и, следовательно, образует конечную булеву алгебру  , которая является подалгеброй булевой алгебры логических функций.
, которая является подалгеброй булевой алгебры логических функций.
Теорема 10.3. Если мощность множества  равна
равна 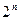
 , то булева алгебра
, то булева алгебра  изоморфна булевой алгебре функций
изоморфна булевой алгебре функций  .
.
Теорема 10.3 указывает на тесную связь между множествами и логическими функциями и позволяет переходить от операций над множествами к операциям над функциями и обратно. В частности, они позволяют непосредственно производить операции над функциями, заданными не формулами, а таблицами. Пример приведён в следующей таблице, содержащей две функции трёх переменных  и
и  и результаты операций над ними:
и результаты операций над ними:
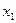 | 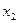 | 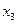 |  |  |  |  |  |
3. ДНФ, интервалы и покрытия.
Теоретико-множественная интерпретация булевой алгебры предлагает очень удобный язык для изучения дизъюнктивных нормальных форм (ДНФ) и построения методов их упрощения. Рассмотрим кратко основные понятия, связанные с ДНФ.
Введём следующее обозначение: обозначим через  множество всех единичных наборов функции
множество всех единичных наборов функции  . Тогда набор (вектор)
. Тогда набор (вектор) 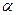 из множества
из множества  принадлежит
принадлежит  тогда и только тогда, когда
тогда и только тогда, когда  . Множество
. Множество  называется единичным множеством функции
называется единичным множеством функции  , а функция
, а функция  называется характеристической функцией множества
называется характеристической функцией множества  . Легко показать, что соответствие между функциями и их единичными множествами является изоморфизмом.
. Легко показать, что соответствие между функциями и их единичными множествами является изоморфизмом.
Если функция 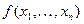 представляется элементарной конъюнкцией всех
представляется элементарной конъюнкцией всех 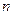 переменных, то множество
переменных, то множество  содержит ровно один элемент множества
содержит ровно один элемент множества  . Если же функция – элементарная конъюнкция
. Если же функция – элементарная конъюнкция 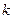 переменных
переменных  , то
, то  содержит
содержит  двоичных наборов. Это объясняется тем, что в таком случае
двоичных наборов. Это объясняется тем, что в таком случае  переменных, не входящих в эту конъюнкцию несущественны для функции
переменных, не входящих в эту конъюнкцию несущественны для функции  . Тогда они принимают
. Тогда они принимают  значений, не изменяя значения
значений, не изменяя значения  . Множество
. Множество  такой функции называется интервалом.
такой функции называется интервалом.
Пример 3. Рассмотрим функцию  и найдём её интервал.
и найдём её интервал.
Прежде всего, заметим, что две переменных  являются несущественными. Это позволяет сразу определить количество единичных наборов, содержащихся в множестве
являются несущественными. Это позволяет сразу определить количество единичных наборов, содержащихся в множестве  (иначе говоря, его мощность). Поскольку в данном случае
(иначе говоря, его мощность). Поскольку в данном случае  , то получим
, то получим  .
.
Далее, очевидно, что 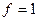 только при значениях
только при значениях  . При этом переменные
. При этом переменные  могут принимать любые значения. Теперь перечислим все единичные наборы для данной функции:
могут принимать любые значения. Теперь перечислим все единичные наборы для данной функции:  . Итак,
. Итак,  .
.
В рассматриваемом случае говорят, что конъюнкция  (или, точнее, интервал
(или, точнее, интервал  ) покрывает множество
) покрывает множество  и все его подмножества.
и все его подмножества.
Представление некоторой функции в виде ДНФ соответствует представлению её единичного множества в виде объединения интервалов; в совокупности все конъюнкции ДНФ покрывают всё единичное множество функции  . Обратное также верно: если все элементы некоторого интервала
. Обратное также верно: если все элементы некоторого интервала  принадлежат
принадлежат  , то существует ДНФ данной функции, содержащая конъюнкцию
, то существует ДНФ данной функции, содержащая конъюнкцию 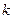 .
.
Назад, в начало конспекта.
 2015-10-22
2015-10-22 3098
3098
