Пусть даны два вектора 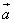 и
и 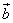 , заданные своими проекциями:
, заданные своими проекциями:
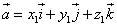
или
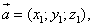
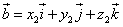
или
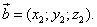
Укажем действия над этими векторами.
1.Сложение:
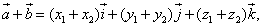
или, что то же
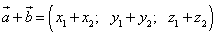 ,
,
т.е. при сложении двух векторов одноимённые координаты складываются.
2.Вычитание:
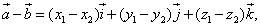
или, что то же
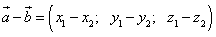 ,
,
т.е. при вычитании двух векторов одноимённые координаты вычитаются.
3.Умножение вектора на число:
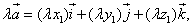
или, что то же
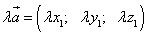 ,
,
т.е. при умножении вектора на число все координаты умножаются на это число.
Пример 5. Даны два вектора:
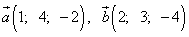 .
.
Найти 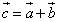 .
.
Решение:
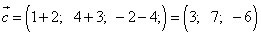 .
.
Пример 6. Даны четыре вектора:
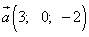 ,
, 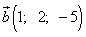 ,
, 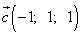 ,
, 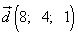 .
.
Найти координаты векторов 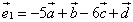 и
и 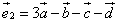 .
.
Решение.
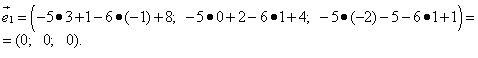 .
.
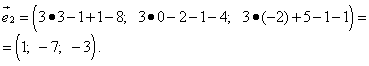 .
.
n - мерные векторы и операции над ними
При изучении многих вопросов, в частности, экономических, оказалось удобным обобщить рассмотренные приёмы установления соответствия между числами и точками двумерного и трёхмерного пространства и рассматривать последовательности n действительных чисел как "точки" некоторого абстрактного " n -мерного пространства", а сами числа - как "координаты" этих точек. За составляющие n -мерного вектора можно принимать такие данные, как урожайность различных культур, объёмы продаж товаров, технические коэффициенты, номенклатура товаров на складах и т.д.
n-мерным вектором называется упорядоченный набор из n действительных чисел, записываемых в виде
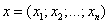 ,
,
где 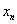 - i – й элемент (или i – я координата) вектора x.
- i – й элемент (или i – я координата) вектора x.
Возможна и другая запись вектора – в виде столбца координат:
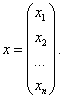
Размерность вектора определяется числом его координат и является его отличительной характеристикой. Например, (2; 5) – двухмерный вектор, (2; -3; 0) – трёхмерный, (1; 3; -2; -4; 7) – пятимерный,
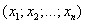 -
-
n – мерный вектор.
Нулевым вектором называется вектор, все координаты которого равны нулю:
0 = (0; 0; …; 0).
Введём операции над n -мерными векторами.
Произведением вектора
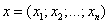
на действительное число 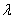 называется вектор
называется вектор
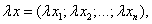
т.е. при умножении вектора на число каждая его координата умножается на это число.
Зная вектор
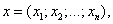
можно получить противоположный вектор
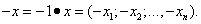
Суммой векторов
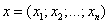
и
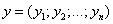
называется вектор
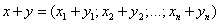 ,
,
т.е. при сложении векторов одной и той же размерности их соответствующие координаты почленно складываются.
Если в плане продаж сети торговых предприятий продажи товаров определить как положительные уровни товаров, а затраты на продажи – как отрицательные, то получим вектор затрат-продаж
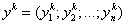 ,
,
где
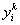 -
-
продажи (затраты) k – м предприятием товара i, а k = 1, 2, 3,…, m.
Суммарный вектор затрат-продаж y определяется суммированием векторов затрат-продаж всех m предприятий сети:
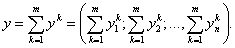
Сумма противоположных векторов даёт нулевой вектор:
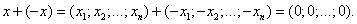
При вычитании двух векторов одной и той же размерности их соответствующие координаты почленно вычитаются:
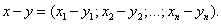
Операции над n -мерными векторами удовлетворяют следующим свойствам.
Свойство 1.
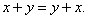
Свойство 2.
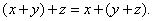
Свойство 3.
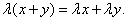
Свойство 4.
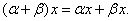
Свойство 5.
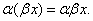
Свойство 6.
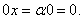
 2015-01-21
2015-01-21 13603
13603








