Статистическое распределение метеорологических величин и его графическое изображение

Климатологический или статистический ряд является первичной формой записи исходных значений метеорологической величины, подготовленных для последующей климатологической обработки. Когда объем статистической совокупности велик, то исходный материал часто представляют в более компактном виде, чтобы составить общее представление о возможных значениях данной метеорологической величины. С этой целью из ряда выбирают наименьшее и наибольшее значение метеорологической величины интервал между ними разбивают на несколько по возможности одинаковых интервалов. Затем подсчитывают, сколько раз случайная величина принимала значения, входящие в каждый интервал (градацию), число случаев или производные от него различные характеристики повторяемости (см. ниже).

Сгруппированную таким образом статистическую совокупность называют статистическим распределением. Записывается статистическое распределение в виде таблицы; в головке или боковике таблицы — градации метеорологической величины, содержание таблицы — повторяемость величины в соответствующих градациях.

Количество градаций составляет, как правило, не менее 5 и не более 15. При выборе градаций для составления распределения одной величины можно руководствоваться таким правилом: количество градаций не должно более чем в 5 раз превышать десятичный логарифм количества наблюдений. Градации не должны перекрывать друг друга и по возможности должны быть равными. Последнее условие не всегда может быть удовлетворено, особенно тогда, когда повторяемость уменьшается очень быстро в какой-то части ряда (осадки, скорость ветра), а также в том случае, когда случайная величина выражается числом дней с явлением. Статистические распределения многомерной или векторной случайной величины (комплекс метеорологических величин) имеют более сложный вид. На практике составляют такие распределения для комплексов, состоящих не более чем из трех величин. Таблица комплекса двух величин имеет два входа: градации первой и второй величины, в содержании таблицы — повторяемость сочетаний значений этих величин, входящих в каждую пару градаций.

Число градаций каждой величины, входящей в комплекс, целесообразно уменьшить, так как в противном случае картина распределения значений комплекса по градациям окажется размытой (повторяемость некоторых сочетаний будет малой).

Приближенную оценку общего числа градаций двойного (К₂) и тройного (К_з) комплекса метеорологических величин можно получить по следующим формулам:

(2.1)

(2.2)

где К₁ —число градаций по одной величине, если она рассматривается отдельно; r — коэффициент корреляции двух величин (в двойном комплексе); R — коэффициент множественной корреляции трех величин.

Например, если для распределения одной величины, рассматриваемой отдельно, принято 5 градаций, а коэффициент корреляции между величинами равен 0,5, то число градаций двойного комплекса в соответствии с формулой (2.1) целесообразно выбирать равным 12—13. Это значит, что при комплексировании каждой величины устанавливаются по 3—4 градации.

Как для одномерных, так и для многомерных величин различают два вида статистических распределений: дифференциальное и интегральное. Вид распределения зависит от вида повторяемости, которая используется для описания характера данного распределения.

Для описания дифференциального распределения используются частота (повторяемость), относительная частота (относительная повторяемость) и сравнительно редко — плотность распределения. Частота статистического распределения одномерной величины m_i * — есть число случаев попадания значений случайной величины в i -ю градацию.

Легко понять, что если объем совокупности или длина статистического ряда равны n, то

где К — число градаций.

Относительная частота определяется как отношение числа случаев со значениями величины, входящими в данную градацию, ко всему объему совокупности. Обозначая относительную частоту i -го интервала для одномерной величины р _i * будем иметь

Из определения следует, что . Относительная частота является оценочным показателем вероятности p данного события (его относительной повторяемости в генеральной совокупности). Согласно теореме Бернулли, при неограниченном увеличении числа наблюдений относительная частота будет приближаться по своей величине к вероятности (теоретической относительной повторяемости). Даже эта начальная обработка климатологического ряда дает важную дополнительную информацию, выделяя, в частности, градации с наибольшей и наименьшей повторяемостью, т. е. наиболее и наименее часто наблюдаемые ситуации. Полезно также иметь в виду, что относительная частота явления или попадания в данную градацию, как правило, может считаться равной доле времени, которое приходится на это явление или градацию. Поэтому, например, данные таблиц 3.1 и 3.12 “Научно-прикладного справочника по климату СССР” следует рассматривать и как долю времени в процентах (а при умножении на продолжительность периода — и в часах), приходящуюся на то или иное направление или градацию скорости ветра.

Используя понятие частоты, можно получить еще один вид: повторяемости — плотность распределения.

Абсолютной (относительной) плотностью распределения называется частота (относительная частота), приходящаяся на единицу ширины градации

(2.4)

где Wa6c и Wотн — соответственно абсолютная и относительная плотности распределения, xi— ширина i-го интервала.

Этот вид повторяемости редко используется на практике, но он является аналогом теоретической плотности р(х), с помощью которой записываются законы распределения непрерывных случайных величин в теории вероятности. При подборе одного из законов для описания распределения метеорологической величины сопоставляются эмпирическая и теоретическая плотности. Последняя является как бы плотностью генеральной совокупности.

Умножая р(х) на ширину интервала Δх, получаем теоретическую частоту m данной градации.

Повторяемость градации обычно относят к ее середине.

В общем виде таблицу статистического дифференциального распределения можно представить так:

Градация	Повторяемость
x0 ‑ x1	m1
x1 ‑ x2	m2
x2 – x3	m3
xk-1 ‑ xk	mk

Нередко вместо границ градаций записывают их середины

а вместо абсолютной повторяемости — относительную.

Установив градацию, необходимо правильно записать ее границы. Строго говоря, полагается записывать границы с большим числом значащих цифр, чем у значений величины, которые встречаются в первичном материале; при этом последний знак не должен быть нулем. Если этого не сделать, то некоторые значения ряда могут совпадать с границами интервалов. Например, если температура воздуха измеряется с точностью до 0,1 °С, то граничные значения должны быть определены с сотыми долями (например, 10,21 °С, но не 10,20 °С). В этом случае ни одно значение температуры не окажется равным граничному, благодаря чему все температуры можно без всяких затруднений распределить по градациям.

Однако в климатологической практике записывать, таким образом, не принято. Обычно левая и правая границы в соседних градациях не повторяются, а отличаются последним знаком. Представляя распределение в окончательном виде, можно сохранить эту привычную для климатологов запись градаций, но проводя расчеты (как по составлению распределения, так и при вероятностном описании распределения), полезно придерживаться формы записи, принятой в статистике, чтобы избежать некоторой неоднозначности.

В качестве примера дифференциального распределения приведем распределение осадков на ст. Свердловск (табл. 2.1).

Суммируя последовательно частоты или относительные частоты градаций, получают накопленные (кумулятивные) частоты (повторяемости).

Таблица 2.1. Дифференциальное распределение месячного количества осадков. Январь, ст. Свердловск; 1937—1950 гг.

Градация количества осадков, мм	m*	р*	Повторяемость
Wабс	Wотн
0,51—5,51		0,143	0,4	0,028
5,51—10,51		0,214	0,6	0,043
10,51—15,51		0,358	1,0	0,072
15,51—20,51		0,214	0,6	0,043
20,51—25,51		0,071	0,2	0,014

Для интегрального распределения используют накопленные частоты. Наращивание частот начинают либо с наименьших, либо с наибольших значений случайной величины в зависимости от решаемой задачи. Таким образом, накопленные частоты, или повторяемости (абсолютная и относительная представляют собой частоты значений случайной величины, не больших или не меньших некоторого заданного значения.

Накопленную частоту (обычно относительную) в метеорологии принято называть обеспеченностью.

Выражения для накопленных частот, или обеспеченностей, имеют вид

(2.5)

(2.6)

где x_i — верхняя граница i-й градации.

Накопленной относительной частоте в теории вероятностей соответствуют значения функции распределения: F (х) =Р(Х < х) или 1-F(x)=P(X x).

В общем виде интегральное статистическое распределение можно записать так:

Граница интервала	Накопленная повторяемость (обеспеченность)
x1	m≤x1
x2	m≤x2
……	…..
xk	m≤xk

Интегральное распределение можно записать иначе, заменив ряд частот m≤x₁ рядом m≥х₁.

В первом случае x_i— правая граница интервала, а во втором— левая.

Примеры интегральных распределений приведены в табл. 2.2 И 2.3.

Таблица 2.2 Таблица 2.3

Интегральное распределение Интегральное распределение

Месячного количества осадков, Месячного количества осадков,

Не большего заданной величины. Не меньшего заданной величины.

Январь, ст. Свердловск; Январь, ст. Свердловск;

1937-1950 гг 1937-1950 гг.

Количество осадков xi
0.51
5.51		0.143
10.51		0.357
15.51		0.714
20.51		0.929
25.51		1.000

Количество осадков xi
0.51		1.000
5.51		0.857
10.51		0.643
15.51		0.286
20.51		0.071
25.51

Интегральное распределение обычно дает более точные результаты по сравнению с дифференциальным.

Если объем исходной выборки невелик (как в приведенном примере или, например, когда ряд составлен из ежегодных максимумов метеорологической величины), то обеспеченности интегрального статистического распределения следует рассчитывать иначе.

Члены ряда размещаются в порядке возрастания (реже — убывания) величины, и каждому значению приписывается обеспеченность, определяемая по формулам: для ряда с возрастающими членами

(2.7)

для ряда с убывающими членами

(2.7')

Здесь x_i — значение члена ранжированного ряда, m_i — номер члена этого ряда, n — общее число членов ряда.

Вместо (2.7) иногда используют (обычно при малом числе членов ряда) следующие формулы:

(2.8)

Или

(2.9)

Если в ряду есть несколько одинаковых членов x_i, имеющих номера , m_i , то и следует рассчитывать не для каждого из них, а только для последнего, и считать (или по формулам (2.8) и (2.9)).

В тех случаях, когда в ряду имеются значения (обычно на концах распределения), резко отклоняющиеся от среднего («отскакивающие» точки от интегральной сглаженной кривой; см. построение интегральных кривых на функциональных сетчатках), используют уточненную формулу вида

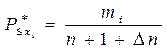(2.10)

Значение Δn обычно подбирают эмпирическим путем. Например, А. М. Мамедов [4] предложил рассчитывать Δn по формуле

(2.11)

где z = f(n, C_v, A), C_v и А — коэффициенты вариации и асимметрии (их определение см. ниже).

В табл. 2.4 приведены значения обеспеченности годовых максимумов скорости ветра, рассчитанные по формуле (2.7).

Обеспеченность в климатологии часто выражается не в долях единицы или в процентах, а в виде частоты (вероятности) повторения явления (например, значений меньше или больше некоторого x_i) в среднем один раз в некоторое число лет (2, 5, 10, 20,..., 50, 100,..., 10 000 и т. д.). Это число лет Т называют в статистике периодом повторения. Формулы перевода обеспеченности в периоды повторения имеют вид

(2.12)

(2.13)

(Переходить к имеет смысл при )

Таблица 2.4. Годовой максимум скорости ветра. Ст. Запорожье

Номер члена ранжированного ряда	Скорость ветра, м/с	Обеспеченность	Номер члена ранжированного ряда	Скорость ветра, м/с	Обеспеченность
		0,19
					0,75
					0,81
		0,37			0,88
					0,94

Формула (2.12) позволяет получить период повторения значений, меньших или равных заданному x_i а формула (2.13) — больших или равных заданному х_i

Естественно, что формулы (2.12) и (2.13) могут применяться не всегда, а только в том случае, если члены ряда каким-то образом характеризуют год и каждый год представлен одним членом ряда. Приведем пример, когда формулы не соответствуют смыслу рассматриваемых параметров.

Пример. Пусть определено, что обеспеченность дней со средней суточной температурой воздуха не ниже 20 °С (t≥20 °С) в июле составляет 0,1, т. е. Р_t≥20 =0,1. Это не значит, что такие дни наблюдаются в среднем один раз в 10 лет. Приведенная обеспеченность получена как отношение числа дней с температурой воздуха t≥20°C к общему числу дней в июле (31). Поэтому среднее число дней m=Р_n = 31 0,1 ≈3 дня. Если Р=0,01, то m=0,3. Это значит, что такие дни наблюдаются в среднем один раз в 3 года (см. также распределение Пуассона).

Следует помнить, что значение P_≤xi- зависит от объема исходной совокупности n. Поэтому нельзя, строго говоря, сравнивать между собой периоды повторения, полученные по P_≥xi данным рассчитанным за разные периоды лет. Используя ранжированные ряды, можно вводить поправку в период повторения при разных объемах статистической совокупности. Методика введения таких поправок изложена в работе [1]. Авторы [1] предлагают формулу

(2.14)

гд а определяется по данным таблицы, часть которой приведена ниже

n
a	0,448	0,443	0,440	0,440	0,439	0,439

С накопленной повторяемостью тесно связано понятие квантилей. Квантиль х_р — есть некоторое значение величины x_i вероятность (частота) непревышения которого равна накопленной повторяемости P_≤xi. Если, например, 30 %-ная квантиль х_зо равна 10°С, то это значит, что в данном статистическом распределении вероятность (частота) появления температуры, не превышающей 10°С, составляет 30%.

Распределение многомерных величин имеет более сложный вид. Рассмотрим распределение двумерной величины (т. е. комплекса двух величин). Двумерное статистическое распределение представляется в виде таблицы с «двумя входами» (табл. 2.5).

Таблица 2.5

Градации y	Градации x	Σ
x0-x1	x1-x2	x2-x3	…	xk-1-xk
y0-y1	m11	m12	m13	…	m1k	m10
y1-y2	m21	m22	m23	…	m2k	m20
…	…	…	…	…	…	…
				…
yl-1-yl	ml1	ml2	ml3	…	mlk	ml0
Σ	m01	m02	m03	…	m0k	n

Абсолютная частота двумерного распределения m_ij есть число попаданий значений одной метеорологической величины в i-й интервал при одновременном попадании соответствующего значения другой величины в i-й интервал.

Относительной частотой двумерного распределения p_i,j служит

(2.15)

где n —число пар значений х и у (объем двумерной совокупности).

Пример двумерного распределения относительных частот представлен в табл. 2.6.

Суммируя последовательно абсолютные или относительные частоты как по строкам, так и по столбцам таблицы двумерного распределения, получают накопленные двумерные частоты 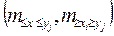относительные частоты

Например, из таблицы можно получить

Таблица 2.6 Двумерное (совместное) распределение (%) срочных значений температуры воздуха и скорости ветра. Январь, ст. Куйбышев

Температура воздуха, 0С	Скорость ветра, м/с
0-2	3-5	6-8	9-11	12-14	15-17	18-20
-35,05 - -30,05	0,2	0,2
-30,05 - -25,05	0,6	1,3	0,7	0,1
-25,05 - -20,05	4,0	6,7	2,7	0,4	0,2
-20,05 - -15,05	5,5	8,0	4,3	1,0	0,2	0,1
-15,05 - -10,05	5,8	11,4	5,1	0,8	0,5	0,2
-10,05 - -5,05	5,8	12,8	5,9	1,2	0,3	0,2
-5,05 - -0,05	2,6	6,0	3,0	0,4	0,2	0,2	0,2
-0,05 – 4,95	0,4	0,4	0,3	0,1

Кроме двумерных частот для двумерного распределения часто рассчитывают также условные частоты.

Трехмерное распределение представляется еще более громоздкой таблицей, чем двумерное, и в климатологической практике такие распределения составляются редко.

Статистические одномерные распределения могут быть представлены в графической форме: либо в виде гистограмм, либо в виде кривых распределения.

Гистограмма дифференциального распределения состоит из прямоугольников, основанием которых являются отрезки между границами градаций, а высотами — повторяемость градаций. Высотами прямоугольников интегральных распределений служит накопленная повторяемость.

Кривая дифференциального распределения строится на основе гистограммы. Она проводится через верхние основания прямоугольников так, чтобы площадь, которую она отсекает от каждого прямоугольника, была равна площади, которую она к нему прирезает (рис. 2.1). Таким образом, сохраняется равенство между площадью гистограммы и площадью, заключенной между кривой распределения и осью абсцисс.

Иногда вместо гистограммы строят полигон (рис. 2.2) — в серединах градаций откладывают повторяемости и точки соединяют прямыми линиями. Полученная ломаная кривая ближе

к сглаженной кривой распределения, чем ступенчатая линия гистограммы. На полигоне не так четко выделяется сама градация. Следует отметить, что если градации не равные, то построение гистограммы и особенно полигона значительно осложняется, так как при переходе к сглаженной кривой площади над ней должны быть пропорциональны частотам в выбираемых градациях. При неравных градациях это соблюсти трудно.

Для построения интегральной кривой распределения наносят точки, соответствующие накопленным повторяемостям, и соединяют их сглаженной линией (рис. 2.3, 2.4).

Дискретные величины правильнее всего изображать в виде диаграммы повторяемостей (рис. 2.5). Иногда повторяемости и для дискретных величин соединяют прямыми линиями (получается полигон), но это не соответствует природе дискретной величины.

Построение гистограммы дифференциального распределения позволяет понять, почему ранее рекомендовалась запись границ градаций с большим числом значащих цифр и повторением одной из границ. Если границы не повторяются, то между прямоугольниками гистограммы образуются промежутки, что затрудняет проведение кривой. Дальше будет показано, что и при подборе к эмпирическим распределениям теоретических законов возникают дополнительные трудности при нестрогой записи границ градаций.

Графиком двумерного распределения могут служить призмограмма или стереограмма (рис. 2.6). В климатологии предпочитают изображать двумерное распределение в координатной плоскости xoy, строя изогипсы поверхностей распределения.