Теоретической базой для математической статистики служит теория вероятностей, которая изучает закономерности случайных явлений в абстрактном виде. На основе этих закономерностей разрабатываются модели или законы распределения случайных величии.
Закон распределения дискретной величины — это задание вероятностей ее возможных значений X = хi. Закон распределения непрерывной случайной величины представляют в виде функции распределения значений X < xi, т. е. в интегральной форме и в виде плотности распределения. Вероятность отдельного значения непрерывной случайной величины равна 0, а вероятность значений, входящих в заданную градацию, равна приращению функции распределения на участке, занимаемом данной градацией Δх.
Каждое теоретическое распределение имеет характеристики, аналогичные характеристикам статистических распределений (математическое ожидание М, дисперсию D, коэффициенты вариации, асимметрии и эксцесса). Эти или другие константы, связанные с ними, носят название параметров распределения.
Подыскание теоретического распределения, соответствующего эмпирическому, или «выравнивание» его является одной из важных задач климатологической обработки. Если найдено и найдено удачно теоретическое распределение, то климатолог получает не только удобную форму представления изучаемой величины, которую можно закладывать в машинные расчеты, но и возможность расчета характеристик, непосредственно не содержащихся в исходном ряду, а также выявления определенных закономерностей. Так, наблюдавшиеся в пункте экстремумы, безусловно, представляют интерес. Однако их появление в имеющейся выборке в значительной степени случайно, поэтому они плохо картируются и иногда существенно различаются на соседних станциях. Если же с помощью найденных распределений определять экстремальные характеристики определенной обеспеченности, то они в значительной мере свободны от указанных недостатков и поэтому являются более представительными. Именно на расчетных экстремумах основаны различные нормативные требования. Поэтому подысканию теоретического распределения и проверке его правильности должно быть уделено особое внимание.
Параметры распределения можно определить разными способами, наиболее точным, но и одновременно сложным является метод максимума правдоподобия. В климатологической практике используется метод моментов.
Статистические характеристики рассматриваются как оценки параметров распределений, характеризующих генеральную совокупность значений данной случайной величины.
Метод моментов определения оценок параметров состоит в следующем. Математическое ожидание, теоретические коэффициенты асимметрии и эксцесса просто заменяются эмпирическим средним и эмпирическими коэффициентами; теоретическая дисперсия равна эмпирической, умноженной на 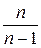 . Если параметрами служат функции моментов, то они вычисляются по эмпирическим моментам.
. Если параметрами служат функции моментов, то они вычисляются по эмпирическим моментам.
Рассмотрим некоторые вероятностные модели, часто используемые в климатологии.
Для дискретных случайных величин используются биномиальные распределения и распределения Пуассона (простое и сложное).
Биномиальное распределение (Бернулли) возникает в результате повторения при постоянных условиях одного и того же испытания, имеющего два исхода: появления или непоявления события (в климатологии, например, отсутствие или наличие явления в каждый день года или месяца).
Случайная дискретная величина понимается при этом как число случаев осуществления некоторого случайного события (явления) из n возможных случаев и может принимать значения 0, 1, 2,..., n.
Аналитическое выражение биномиального закона распределения имеет вид  (5.1)
(5.1)
где

Закон определяет вероятность того, что событие, вероятность которого р, будет наблюдаться х раз при n испытаниях. Например, в климатологии день может быть либо с явлением, либо без явления (с туманом, с определенным количеством осадков, температурой воздуха определенных градаций и т. д.). Во всех этих случаях возможны два исхода, и на вопрос, сколько раз будет наблюдаться событие (например, день с туманом), ответ можно получить с помощью биномиального закона (5.1). При этом р принимается равным р*, т. е. относительной частоте — отношению числа случаев с явлением к общему числу случаев (формула (2.3)).
Например, если рассматривается число дней с туманом в августе и по многолетнему ряду установлено, что в среднем в августе бывает 5 дней с туманом, то относительная частота (вероятность) дня с туманом в августе {31 день) равна

Параметрами биномиального распределения являются n и р, которые связаны с математическим ожиданием (средним значением), средним квадратическим отклонением, коэффициентами асимметрии и эксцесса этого распределения следующими выражениями:
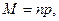


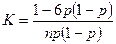
На рис. 5.1 приведены графики биномиального распределения при разных параметрах n и р.

Рассчитаем, например, пользуясь биномиальным законом, вероятность того, что в августе на станции будет наблюдаться три дня с туманом, если вероятность образования тумана в любой день августа (т. е. отношение среднего числа дней с туманом в августе к общему числу дней за месяц) составляет 0,16.
Так как n= 31, а 1 — р = 0,84, по формуле (5.1) получим


p(3)=0.1334≈0.13
Пределом биномиального распределения при условии, что рассматриваются маловероятные события в длинной серии независимых испытаний (наблюдений), является распределение Пуассона.
Случайная величина, распределенная по закону Пуассона, может принимать ряд значений, образующих бесконечную последовательность целых чисел 0, 1, 2, ∞ с вероятностью 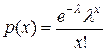
где λ. —параметр, являющийся математическим ожиданием распределения.
Закон определяет вероятность того, что случайная величина будет наблюдаться х раз, если среднее ее значение (математическое ожидание) равно λ.

Обратим внимание на то, что параметром биномиального закона служит вероятность события р, и поэтому надо указать, из какого общего количества случаев n определяется вероятность р(х). В законе Пуассона параметром является среднее число случаев λ за рассматриваемый период, поэтому продолжительность периода непосредственно не входит в формулу.
Дисперсия распределения Пуассона и третий центральный момент равны математическому ожиданию, т. е. тоже равны λ.
При больших различиях между средним и дисперсией законом Пуассона пользоваться нельзя. Распределение Пуассона затабулировано и приводится во всех сборниках статистических таблиц, справочниках и учебниках по статистике. На рис. 5.2 приведено распределение числа дней с грозой (редкое событие) по закону Пуассона. Для Архангельска за год λ,= 11 дней и за июль λ = 4 дня. Как видно из рис. 5.2, в Архангельске вероятность восьми дней с грозой в июле составляет примерно 0,03, а вероятность восьми дней в году —около 0,10. Обратим внимание на одно обстоятельство. Часто среднее число дней с явлением в году λ при λ≤1 трактуют как величину, обратную периоду повторения T (например, λ= 0,3 — один день в три года, λ = 1-практически ежегодно).
Такой «осредненный» подход чреват ошибками, тем большим, чем больше λ. Даже если дни с явлением не связаны между собой, вероятны годы не с одним, а с несколькими днями. В результат соотношение Т = 1/λ оказывается неправильным. Так, при λ= 1 явление, как легко убедиться из формулы закона Пуассона, наблюдается не ежегодно, а только в 6—7 годах из 10. Вероятность того, что в году явление наблюдаться не будет, равна вероятности, что будет один день с явлением (0,37) и почти такая же, как вероятность, что будет два и более дней. Только при λ≤ 0,2 указанным соотношением можно пользоваться с достаточным основанием; потому что вероятность двух и более дней в году в этом случае менее 0,02 (реже, чем один раз в 50 лет).
Применение закона Пуассона к редким метеорологическим явлениям не всегда оказывается полезным. Например, иногда редкие явления могут следовать одно за другим вследствие того, что условия, их вызывающие, сохраняются длительное время, и условия закона Пуассона не выполняются.
Больше соответствует природе редких метеорологических явлений сложное распределение Пуассона (отрицательное биномиальное распределение). Оно возникает, когда ряд явлений можно рассматривать как значения разных случайных величин (выборки из разных генеральных совокупностей). Все эти величины имеют распределение Пуассона, но с разными параметрами λ1, λ2..., λk.
Сложное распределение Пуассона зависит с одной стороны от распределения совокупности параметров, а с другой — от распределения каждой из величин. Выражение для вероятности в случае данного распределения имеет вид
 (5.2)
(5.2)
или в более удобной для расчетов форме

Математическое ожидание М и дисперсия D этого распределения связаны с его параметрами γ и λ формулами
 (5.3)
(5.3)
Заменяя величины М и D их оценками  и
и  , получим
, получим
 (5.4)
(5.4)
Расчеты p(x) можно упростить, пользуясь тем, что существует равенство
 , (5.5)
, (5.5)
при x=0
 . (5.6)
. (5.6)
Следовательно,

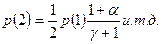
Пример расчета. Рассчитаем распределение числа дней с сильным ветром на ст. Чулым для июля, если  =1 день, σ=1,7 дня. Определим α и γ:
=1 день, σ=1,7 дня. Определим α и γ:
α≈ 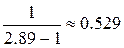
γ≈ 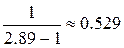
Вероятность того, что не будет ни одного дня с сильным ветром, составит
p(0)= 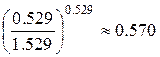
Вероятность того, что будет один день с сильным ветром, равна p(1)=  . График сложного распределения Пуассона представлен на рис. 5.3.
. График сложного распределения Пуассона представлен на рис. 5.3.
Для непрерывных случайных величин в климатологии чаще всего используются нормальное, логнормальное распределения, распределение Шарлье, гамма-распределение, распределения Вейбулла и Гумбеля, а также композиционный закон нормальной и равномерной плотности.
Наибольшее теоретическое и практическое значение имеет нормальный, или гауссовский, закон распределения. Этот закон является предельным для многих других теоретических распределений и образуется тогда, когда каждое значение случайной величины можно рассматривать как сумму достаточно большого числа независимых случайных величин.
Нормальный закон задается выражениями для плотности и функции распределения вида
 (5.7)
(5.7)
 (5.8)
(5.8)
где  и σ — параметры распределения — среднее значение и среднее квадратическое отклонение данной величины. Кривая плотности нормального распределения симметрична и одновершинна.
и σ — параметры распределения — среднее значение и среднее квадратическое отклонение данной величины. Кривая плотности нормального распределения симметрична и одновершинна.

Для расчетов по этим формулам, прежде всего, вводят новую вспомогательную переменную t, приводя нормальный закон к стандартному виду с М = О, D = 1.
Величина t рассчитывается по формуле
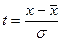 (5.9).
(5.9).
а функция стандартного нормального распределения имеет вид
F(t)=P(T<t)=  (5.10)
(5.10)
Или
 (5.11)
(5.11)
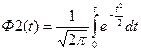 (5.12)
(5.12)
Значения Ф(t) приводятся в любом справочнике по высшей математике.
Выражая функцию распределения через вспомогательную функцию, так называемый интеграл вероятностей, получим вероятность попадания значений случайной величины
в закрытый интервал'
Р (X1 < X < Х2) = ½(Ф1(t2) – Ф1(t1)], (5.13) Р (Х1 < X < Х2) = Ф2 (t2) – Ф2 (t1,); (5.14)
в открытый интервал (с учетом того, что 
 (5.15)
(5.15)
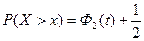 (5.16)
(5.16)
 (5.16а)
(5.16а)
В открытый интервал (с учетом того, что  )
)
Пример расчета вероятностей нормального распределения для  = 14,35 °С и σ = 1,348 °С представлен в табл. 5.1.
= 14,35 °С и σ = 1,348 °С представлен в табл. 5.1.
Таблица 5.1
Рабочая таблица для расчета распределения средней месячной температуры воздуха в июне и июле за 100 лет
| Градация температуры | Граница градации | ti | Ф2(ti) | P(Xi<X<Xi+1) |
| воздуха, ºС | ||||
| ≤12,55 | 12,55 | —1,34 | —0,4180 | 0,0820 |
| 12,55... 13,05 | 13,05 | —0,97 | —0,3340 | 0,0840 |
| 13,05... 13,55 | 13,55 | -0,60 | —0,2257 | 0,1083 |
| 13,55... 14,05 | 14,05 | —0,22 | —0,0871 | 0,1386 |
| 14,05... 14,55 | 14,55 | 0,15 | 0,0596 | 0,1467 |
| 14,55... 15,05 | 15,05 | 0,52 | 0,1985 | 0,1389 |
| 15,05... 15,55 | 15,55 | 0,90 | 0,3159 | 0,1174 |
| 15,55... 16,05 | 16,05 | 1,27 | 0,3980 | 0,0821 |
| 16,05... 16,55 | 16,55 | 1,64 | 0,4495 | 0,0515 |
| ≥16,55 | 0,4495 | 0,0505 |
График рассчитанного распределения приведен на рис. 5.4.
Во многих случаях эмпирические распределения хорошо описываются нормальным законом в пределах 2σ — 2,5σ от  , но отступают от него в крайних точках. Здесь надо учитывать большую относительную погрешность определения малых р (см. ниже) и случайность попадания крупной аномалии в имеющуюся выборку. В этих случаях «спрямление» эмпирического распределения вполне обосновано. Но могут быть и реальные отклонения на краях.
, но отступают от него в крайних точках. Здесь надо учитывать большую относительную погрешность определения малых р (см. ниже) и случайность попадания крупной аномалии в имеющуюся выборку. В этих случаях «спрямление» эмпирического распределения вполне обосновано. Но могут быть и реальные отклонения на краях.
Поэтому необходима тщательная проверка, привлечение данных соседних по возможности более длиннорядных станций.

В связи с рассмотрением нормального распределения необходимо остановиться на правиле «трех сигм». Суть правила сводится к следующему: поскольку при нормальном распределении вероятность отклонения от х более чем на Зо1 составляет 0,003, тс такие данные с большой степенью достоверности можно считать ошибочными, и они подлежат браковке. Необходимо сразу оговориться, что в климатологии к правилу «трех сигм» нужно относиться с большой осторожностью. Даже если распределение нормально, то (хотя вероятность отдельного конкретного случая большого отклонения действительно очень мала) при большом количестве наблюдений вероятность становится достаточно значимой. Так, при 100 измерениях вероятность хотя бы одного отклонения больше За составляет около 30 %. Если распределение симметрично, но эксцесс К > 0, то, как отмечалось выше, за пределами За лежит не 0,3%, а несколько процентов наблюдений. И самое главное, аномалия, если она действительно наблюдалась, имеет наиболее существенное значение. Поэтому прежде чем отвергнуть какие-нибудь данные, необходима самая тщательная проверка. Правило «трех сигм» может быть только сигналом необходимости такой проверки. Сама проверка должна основываться на другом (сравнение с соседними пунктами, сроками, показаниями других приборов и др.).
Нормальным распределение не может быть для тех случайных величин, значения которых снизу или сверху ограничены некоторым легко достижимым в естественных условиях физическим пределом, например, скорость ветра v = 0 м/с, относительная влажность 100%, количество облачности 0 и 10 баллов. Кривая нормального распределения показана на рис. 5.4. Нормальное распределение является симметричным.
В отличие от нормального логнормальное распределение формируется тогда, когда каждое значение случайной величины можно рассматривать не как сумму, а как произведение большого количества независимых случайных величин. В этом случае нормально распределяется логарифм случайной величины. Функция логнормального распределения имеет вид

Для того чтобы воспользоваться этим выражением, надо определить его параметры 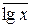 и σlgx. Но так как такие параметры в справочниках отсутствуют, то для этой цели выбирается способ, который позволяет использовать известные характеристики: среднее, среднее квадратическое отклонение σи коэффициент асимметрии A. Расчеты обеспеченности и квантилей проводятся в следующей последовательности:
и σlgx. Но так как такие параметры в справочниках отсутствуют, то для этой цели выбирается способ, который позволяет использовать известные характеристики: среднее, среднее квадратическое отклонение σи коэффициент асимметрии A. Расчеты обеспеченности и квантилей проводятся в следующей последовательности:
1) определяется вспомогательный параметр ω
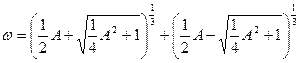 (5.17)
(5.17)
2) рассчитывается среднее квадратическое отклонение значений вспомогательной величины у
 (5.18)
(5.18)
3) для значения величины х, обеспеченность которой надо
определить, рассчитывается величина t
 (5.19)
(5.19)
4) по таблице интеграла вероятностей находим Ф(t), а затем
рассчитываем обеспеченность Р (X ≤ х0) по формуле
 (5.19а)
(5.19а)
Пример расчета. Рассчитать обеспеченность месячной суммы осадков 1 см, если среднее многолетнее количество осадков составляет 4,23 см,  =2,33 см, A = 0,46:
=2,33 см, A = 0,46:


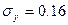

Ф(t)=-0.864

Кривые логнормального распределения при различных σ (для наиболее простого вида логнормальных распределений) изображены на рис. 5.5. Как правило, это асимметричное распределение.
Не резко асимметричным является распределение Шарлье, которое иногда называется обобщенным нормальным распределением и используется примерно в тех же случаях, что и нормальное распределение.

Плотность распределения Шарлье получают, разлагая в ряд плотность вероятности нормального закона или закона Пуассона. В первом случае вероятность значений случайной величины в интервале xi, xi+1 можно рассчитать по формуле

где А и К — коэффициенты асимметрии и эксцесса соответственно, Ф(ti)-интеграл вероятности нормального закона, Bi и Сi - коэффициенты.
Пример задачи выравнивания эмпирического распределения скорости ветра с помощью распределения Шарлье приведен в табл. 5.2. В таблице приведены эмпирические частоты mi; по градациям скорости ветра;  = 2,1 м/с, σ = 9,9 м/с, A= 0,38, К = 0,34. В результате выравнивания получены теоретические частоты
= 2,1 м/с, σ = 9,9 м/с, A= 0,38, К = 0,34. В результате выравнивания получены теоретические частоты 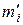 . Сопоставление mi и
. Сопоставление mi и 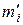 дает оценку того, насколько хорошо подходит к данному случаю распределение Шарлье. Если различия будут признаны допустимыми, то в дальнейшей работе можно использовать взятое распределение. (Теоретическая оценка допустимости различий приведена ниже.)
дает оценку того, насколько хорошо подходит к данному случаю распределение Шарлье. Если различия будут признаны допустимыми, то в дальнейшей работе можно использовать взятое распределение. (Теоретическая оценка допустимости различий приведена ниже.)
Таблица 5.2 Выравнивание по распределению Шарлье. Скорость ветра на уровне 6 км. Ст. Минск
| Скорость ветра (xi) м/с | mi |  |  |  | ABi10³ | ABi10³ | nФ2(t)+ +ABi+KCi | p'i | m'i |
| <0 | –2,12 | –0,4830 | 9,3 | 1,9 | ‑0,4718 | ||||
| 0–5,5 | 0,036 | ‑1,57 | –0,4418 | –0,8 | –1,4 | –0,4540 | 0,0364 | ||
| 5,5–11.5 | 0,156 | –0,96 | –0,3314 | 1,2 | –7,1 | –0,3373 | 0,1167 | ||
| 11,5–17,5 | 0,180 | –0,35 | –0,1368 | 20,8 | -5,4 | –0,1214 | 0,2159 | ||
| 17,5–23,5 | 0,226 | 0,25 | 0,0987 | 23,0 | 4,0 | –0,1257 | 0,2471 | ||
| 23,5-29,5 | 0,226 | 0,86 | 0,3051 | 4,6 | 7,6 | -0,3173 | 0,1916 | ||
| 29,5-35,5 | 0,114 | 1,47 | 0,4292 | –9,9 | 2,4 | 0,4217 | 0,1044 | ||
| 35,5–41,5 | 0,032 | 2,07 | 0,4808 | –9,7 | –1,7 | 0,4694 | 0,0477 | ||
| 41,5–47,5 | 0,019 | 2,68 | 0,4963 | –4,3 | –1,7 | 0,4903 | 0,0216 | ||
| 47,5-53,5 53.5-59.5 Σ | 0,006 0.005 1.000 | 3,28 3.89 - | 0,4995 0.4999 - | –1,1 -0.2 - | –0,7 -0.1 - | 0,4977 0.4996 - | 0,0074 0.0012 0.9900 |
Рис. 5.6. Распределение скорости ветра на высоте 6 км.
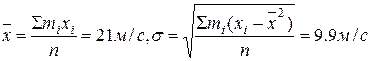

График этого распределения приведен на рис. 5.6.
Асимметричным распределением, близким к логнормальному, является гамма-распределение.
Плотность вероятности двухпараметрического гамма-распределения имеет вид
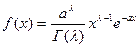 (5.20)
(5.20)
трехпараметрического —
 (5.21)
(5.21)
Математическое ожидание, дисперсия и коэффициенты асимметрии и эксцесса гамма-распределения связаны с параметрами a и λв первом случае соотношениям  (5.22) (5.22)
(5.22) (5.22)
Откуда 
при этом М=  .
.
Вводится новая переменная u, равная ах, от которой затем следует перейти ко второй новой переменной t равной  . В сборнике статистических таблиц, например, Е. Е. Слуцкого: («Таблицы неполной гамма-функции». Изд. АН СССР, 1950) по. Значениям p(t,2λ). определяются значения функции p(t, 2λ), которая связана с интегральной функцией
. В сборнике статистических таблиц, например, Е. Е. Слуцкого: («Таблицы неполной гамма-функции». Изд. АН СССР, 1950) по. Значениям p(t,2λ). определяются значения функции p(t, 2λ), которая связана с интегральной функцией
 (5.23)
(5.23)
Порядок вычислений представлен в табл. 5.3.
Таблица 5.3
Выравнивание по гамма-распределению. Месячное количество осадков, май, ст. Земетчино
| Количество осадков, см | mi |  | ui | ti | P(t,2λ) | F(u) | p' | m'i | |
| 0–1,05 | 0,067 | 0,79 | –1,90 | 0,975 | 0,025 | 0,025 | |||
| 1,05-2,05 | 0,120 | 1,58 | –1,06 | 0,825 | 0,175 | 0,150 | |||
| 2,05–3,05 | 0,133 | 2,36 | –0,60 | 0,670 | 0,330 | 0,155 | |||
| 3,05–4,05 | 0,147 | 3,15 | –0,14 | 0,483 | 0,517 | 0,187 | |||
| 4,05–5,05 | 0,160 | 3,94 | 0,29 | 0,324 | 0,676 | 0,159 | |||
| 5,05–6,05 | 0,173 | 4,73 | 0,67 | 0,206 | 0,794 | 0,118 | |||
| 6,05–7,05 | 0,080 | 5,51 | 1,02 | 0,129 | 0,871 | 0,077 | |||
| 7,05–8,05 | 0,053 | 6,30 | 1,34 | 0,072 | 0,928 | 0,057 | |||
| 8,05–9,05 | 0,027 | 7,10 | 1,65 | 0,043 | 0,957 | 0,029 | |||
| 9,05–10,05 | 0,013 | 7,88 | 1,94 | 0,024 | 0,976 | 0,019 | |||
| 10,05–11,05 | 0,027 | 8,66 | 2,21 | 0,013 | 0,987 | 0,011 | |||
| Σ | |||||||||

Функция распределения Вейбулла имеет вид
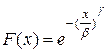 (5.24)
(5.24)
Где β и γ— параметры распределения Вейбулла, связанные с  и σ следующим образом:
и σ следующим образом:
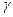 | 1,0 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 |
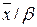 | 1,00 | 0,96 | 0,94 | 0,92 | 0,91 | 0,90 | 0,90 | 0,89 | 0,89 | 0,89 | 0,89 |
 | 1,00 | 0,91 | 0,83 | 0,78 | 0,73 | 0,68 | 0,64 | 0,61 | 0,58 | 0,56 | 0,53 |
Зная  и σ,c помощью элементарного расчета можно получить значения β и γ
и σ,c помощью элементарного расчета можно получить значения β и γ
Обычно приведенное выше уравнение (5.24) решают графически (см. раздел 8). Тогда при определении вероятности значений случайной величины, больших заданного, можно обойтись без параметров β и γ.
Функция распределения Гумбеля имеет вид
 (5.25)
(5.25)
Связь между y и x0 задается формулами
 (5.26)
(5.26)
где х и  — среднее и дисперсия ряда максимумов случайной величины;
— среднее и дисперсия ряда максимумов случайной величины; 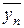 и
и  — среднее и дисперсия ряда вспомогательной величины, которые определяются по формулам
— среднее и дисперсия ряда вспомогательной величины, которые определяются по формулам  ,(5.27)
,(5.27)
 (5.28)
(5.28)
Значения  представлены в табл. 5.4;они зависят от числа членов ряда.
представлены в табл. 5.4;они зависят от числа членов ряда.
Таблица 5.4 Данные для определения значений  по числу членов рядa.
по числу членов рядa.
| n | 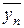 | σn | n | 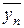 | σn |
| 0,4952 | 0,9497 | 0,5220 | 1,0565 | ||
| 0,4996 | 0,9676 | 0,5236 | 1,0626 | ||
| 0,5085 | 0,9833 | 0,5252 | 1,0796 | ||
| 0,5070 | 0,9972 | 0,5268 | 1,0754 | ||
| 0,5100 | 1,0095 | 0,5283 | 1,0811 | ||
| 0,5128 | 1,0206 | 0,5296 | 1,0864 | ||
| 0,5157 | 1,0316 | 0,5309 | 1,0914 | ||
| 0,5181 | 1,0411 | 0,5569 | 1,1938 | ||
| 0,5202 | 1,0493 | 0,5600 | 1,2065 |
Для того чтобы не проводить трудоемких расчетов по формуле (5.25), можно воспользоваться табл. 5.5.
Таблица 5.5
| Обеспеченность F(х), % | 0,1 | 0,04 | 0,01 | ||||||
| Число лет | |||||||||
| у | 0,37 | 1,50 | 2,25 | 2,97 | 3,90 | 4,60 | 6,91 | 7,82 | 9,21 |
С помощью распределения Гумбеля решается задача о нахождении обеспеченности больших скоростей ветра (X ≥ x0) или обратная задача: по заданной обеспеченности найти соответствующую скорость ветра. В первом случае по x0 и по формуле (5.26) находим у и по табл. 5.5 определяем F(x0); во втором случае по F(x0) из табл. 5.5 определяем у и по формуле (5.26) находим с: ответствующее х0. В обоих случаях  и σx берем из условий задачи, а
и σx берем из условий задачи, а  — из табл. 5.4 по заданному ряду наблюдений.
— из табл. 5.4 по заданному ряду наблюдений.
Значение n определяется как удвоенный объем выборки, использованный для определения максимума.
Пример расчета. Рассчитать скорость ветра, возможную один раз в 1000 лет, если  = 20 м/с, σx = 4 м/с, полагая, что значение
= 20 м/с, σx = 4 м/с, полагая, что значение  определялось по выборке 40 лет, т. е. n = 80,.
определялось по выборке 40 лет, т. е. n = 80,.
Зная число членов ряда n, по табл. 5.4 определяем значения 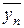 и σn, которые равны соответственно
и σn, которые равны соответственно 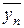 — 0,5569, σn = 1,1938; затем по табл. 5.5 определяем значение у = 6,91. Тогда
— 0,5569, σn = 1,1938; затем по табл. 5.5 определяем значение у = 6,91. Тогда
x0 = 
При композиции нормального закона с плотностью

и закона равномерной плотности в интервале от а до b

Формула плотности вероятности имеет следующий вид:
 =
=  (5.29)
(5.29)
где а и b — параметры равновероятного закона,  —дисперсия нормального закона.
—дисперсия нормального закона.
Если задано статистическое распределение метеорологической величины, то для композиции нормального и равновероятного распределений пользуются формулами
 =
= 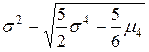
 (5.30)
(5.30)
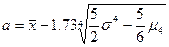
где  и σ² — среднее и дисперсия эмпирического распределения, μ4 -центральный момент 4-го порядка:
и σ² — среднее и дисперсия эмпирического распределения, μ4 -центральный момент 4-го порядка:
 .
.
Пример расчета. Рассчитать число случаев попадания в указанные в табл. 5.6 градации температуры воздуха (графа 1) по композиции закона Гаусса и равномерной вероятности, если задано эмпирическое распределение температуры воздуха (табл. 5.6, графа 4). В табл. 5.6 показан порядок вычисления параметров 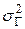 , a и b.
, a и b.
Для этого переходят к условным единицам х'i: из середины каждого интервала xi (графа 2) вычитается середина центральной градации (х0 = 11) или градации, имеющей наибольшую частоту, и результат делится на ширину интервала h = 2, т. е. x'i= (xi—x0)/h (графа 3).
По распределению температуры, выраженной в условных единицах, определяются  и μ4.
и μ4.


По формулам (5.30) определяются параметры композиционного закона:

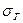 = 1,352,
= 1,352,
b = 0,44 +  1 = 3,00,
1 = 3,00,
а = 0,44 —  = -2,12.
= -2,12.
От значений х' переходят к значениям новой переменной t по формулам

и заполняют графы 9 и 10 в табл. 5.6. Для ti и tj находят значение интегралов вероятности (Ф1(ti) и Ф1(tj), а также их разность. Вероятность попадания значений температуры в градации рi 'определяется по формуле

h' — градация для переменной х' в условных единицах, (равна единице). 
В последнее время помимо распределений отдельных (одномерных) случайных величин используются и некоторые распределения двух- и трехмерных величин (или случайных векторов). Необходимость в использовании этих достаточно сложных распределений возникла в связи с большим значением для прикладных целей распределений комплексов метеорологических величин.
Чаще других многомерных распределений используются логнормальные и многомерная конструкция Гумбеля. Плотность логнормального распределения через вспомогательные переменные u и v выражается в виде
 (5.31)
(5.31)
где  с помощью приведенных ниже формул определяются через средние значения температуры tср и относительной влажности fср, их средние квадратические отклонения σt, σf, коэффициенты асимметрии At, Af и корреляции rtf.
с помощью приведенных ниже формул определяются через средние значения температуры tср и относительной влажности fср, их средние квадратические отклонения σt, σf, коэффициенты асимметрии At, Af и корреляции rtf.
Если 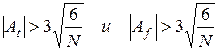 , где N — общее число наблюдений, то вычисляем следующие параметры:
, где N — общее число наблюдений, то вычисляем следующие параметры:
 (5.32)
(5.32)
 (5.33)
(5.33)
 (5.34)
(5.34)
 (5.35)
(5.35)
 (5.36)
(5.36)
 (5.37)
(5.37)
 (5.38)
(5.38)
 (5.39)
(5.39)
 (5.40)
(5.40)
 (5.41)
(5.41)
 (5.42)
(5.42)
где t, f в формулах (5.41) и (5.42) являются серединами градации соответственно температуры и относительной влажности, нормированными (деленными) на величину градации. Если параметры определены и распределение g (u, v) построено, то вероятность градации (t, f) равна

где u и v определяются по (5.41) и (5.42).
Если  тогда ωt не вычисляем. Полагаем
тогда ωt не вычисляем. Полагаем  . Параметры ωf, σv,
. Параметры ωf, σv,  вычисляются по формулам (5,35) —(5.37);
вычисляются по формулам (5,35) —(5.37);

Параметр а не вычисляется, а параметр b рассчитывается л формуле (5.40);

Вероятность в этом случае рассчитывается по формуле

Если 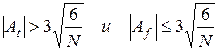 то параметры ωt, σu,
то параметры ωt, σu,  вычисляются по формулам (5.32) — (5.34). Параметр ωf не вычисляем, полагаем
вычисляются по формулам (5.32) — (5.34). Параметр ωf не вычисляем, полагаем

Параметр а определяем по формуле (5.39), а параметр b не вычисляем;

Вероятность p(t, f) определяется по формуле
 .
.
В случае когда  , полагаем
, полагаем
 . Величины ωt и ωf не вычисляются.
. Величины ωt и ωf не вычисляются.
Параметры а и b также не вычисляются. Полагаем u = t, v = f.
Вероятность p(t, f) вычисляется по формуле
p(t, f)=g(u, v).
Другими словами, плотность логнормального распределения в этом случае равна плотности нормального распределения.
Пример расчета. Распределение (%) температуры и относительной влажности воздуха. Ст. Татарск, июнь, 13 ч (1899—1917, 1924—1960 гг.—всего 1304 случая)
| Температура воздуха, °С | Относительная влажность, % | |||||
| Σ | ||||||
| 0-19 | 20-39 | 40-59 | 60-79 | 80-100 | ||
| 0,0... 4,9 | 0,1 | 0,2 | 0,3 | |||
| 5,0... 9,9 | 0,1 | 0,6 | 1,2 | 1,4 | 3,3 | |
| 10,0... 14,9 | 1,5 | 5,4 | 4,4 | 3,3 | 14,6 | |
| 15,0... 19,9 | 7,4 | 12,2 | 6,7 | 2,1 | 28,4 | |
| 20,0... 24,9 | 0,3 | 10,1 | 12,1 | 5,0 | 0,2 | 27,7 |
| 25,0... 29,9 | 0,4 | 12,0 | 6.9 | 0,8 | 0,1 | 20,2 |
| 30,0... 34,9 | 0,5 | 3,9 | 0,5 | 0,1 | 0,1 | 5,1 |
| 35,0... 39,9 | 0,2 | 0,2 | 0,4 | |||
| Σ | 1,4 | 35,2 | 37,7 | 18,3 | 7,4 | 100,0 |
Рассмотрим возможность представить это распределение двумерным логнормальным распределением. Для этого вычислим статистические  характеристики данного распределения температуры и влажности:
характеристики данного распределения температуры и влажности:
 В данном случае
В данном случае

Вычисляем ωt по формуле (5.35): ωf=0,175; σv и  - по формулам (5,36) и (5,37): σv=0.173,
- по формулам (5,36) и (5,37): σv=0.173, 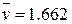 ;
;

Вычисляем, например, вероятность градации 15,0-19,9ºС, 20-39%, ht=5.0ºC, hf=20,0%-размеры градации по температуре и относительной влажности соответственно:


Фактическая повторяемость этой градации равна 0,074.
Конструкция Моргенштерна — Гумбеля для функции двумерного распределения имеет вид
 , где F(x) и G(y)— одномерные функции распределения соответственно для переменных х и у. Параметр α связан с коэффициентом корреляции между элементами комплекса и при отсутствии связи между ними равен нулю.
, где F(x) и G(y)— одномерные функции распределения соответственно для переменных х и у. Параметр α связан с коэффициентом корреляции между элементами комплекса и при отсутствии связи между ними равен нулю.
Вероятность попадания в градации (xi, xi+1) (yj, yj+1) можно рассчитать по формуле

В отделе фондов алгоритмов и программ (ОФАП) ВНИИГМИ-МЦД имеется программа Ж 051050986, которая позволяет рассчитать двумерную и трехмерную функцию распределения Моргенштерна — Гумбеля. Для расчетов по этой программе можно пользовать два варианта входных данных.
По первому варианту расчетов в конструкцию Гумбеля соединяются два или три эмпирических распределения компонентов комплекса. При этом для точных расчетов входными параметрами служат также коэффициенты корреляции между компонентами. Если последние характеристики отсутствуют, то значения α можно принять равными единице. По второму варианту расчетов сначала необходимо выбрать теоретические законы распределения для компонентов комплекса входными параметрами служат параметры этих распределений и, кроме того, коэффициенты корреляции между ними, те же, как и в предыдущих случаях. В конструкцию Гумбеля можно, например, объединить два или три логнормальных распределения (месячные распределения температуры и влажности), композиции нормального и равновероятного распределения температуры энтальпии за год и т. д.
Пример расчета. Рассчитать вероятность сочетания температуры воздуха -25...-20°С и скорости ветра 3—5 м/с по распределениям температуры и скорости ветра, приведенным ниже:
| Температура, °С Повторяемость, % F(xi) F(xi+1)+F(xi) | -35…-30 0.5 0.5 | -30…-25 1.3 1.8 2.3 | -25…-20 4.6 6.4 8.2 | -20…-15 11.0 17.4 23.8 | ||||
| Скорость ветра, м/с Повторяемость, % F(xi) F(xi+1)+F(xi) | 0-2 14,7 14,7 - | 3-5 33,2 47,9 62,6 | 6-8 26,5 74,4 122,3 | 9-11 10,6 85,0 159,4 | 12-14 9,1 94,1 179,1 | 15-17 4,9 99,0 193,1 | 18-20 1,0 199,0 | |
Вероятность заданного сочетания в долях единицы равна:
р (—25... —20; 3 — 5) = (0,046· 0,332) [1 + (0,082—1) (0,626— 1)] =
= 0,018, или 1,8 %. Эмпирическая вероятность этого сочетания равна 1,5 %.
Более сложные случаи расчета следует выполнять на ЭВМ по указанной программе.
Заключая рассмотрение законов распределения, используемых для описания распределений метеорологических величин, можно систематизировать эти распределения по соответствующим законам распределения (табл. 5.7)
Таблица 5.7
Некоторые наиболее часто используемые метеорологические распределения и законы распределения, удобные для их выравнивания
| Климатологический элемент | Закон распределения | Примечание |
| 1.Температура воздуха | ||
| средняя суточная средние суточные максимум и минимум | Почти нормальное Шарлье | В Восточной Сибири положительная асимметрия, в ЕЧС отрицательная асимметрия зимой. |
| срочная температура | Композиция нормального и равномерной плотности Гумбеля | В годовой совокупности «срочных» наблюдений |
| годовые и месячные экстремальные значения | ||
| даты первых и последних заморозков | Нормальное | |
| 2. Осадки | ||
| годовые суммы | Почти нормальное гамма-распределение | Распределение приближается к нормальному по мере возрастания периода наблюдений.. |
| Продолжительность осадков (от недельных до сезонных) | Нормальное | Положительная асимметрия |
| годовые экстремумы | Гумбеля | |
| число дней с осадками | Сложное Пуассона | |
| Повторяемость ливневых осадков | Пуассона | |
| Число дней с градом, грозой | Биномиальное | Если явление наблюдается часто |
| Число дней с явлением | Пуассона | Если явление наблюдается редко |
| Среднее годовое число дней с явлением | Отрицательное биномиальное | |
| 3. Давление | ||
| среднее месячное и годовое | Нормальное | |
| среднее суточное | Почти нормальное, Шарлье | |
| среднее часовое | ||
| 4. Влажность | ||
| среднее годовое парциальное давление пара | Нормальное, Шарлье | Положительная асимметрия |
| относительная влажность | Шарлье, нормальное | V-образное распределение |
| количество облаков | Пирсона (I тип кривой), биномиальное | |
| 5. Ветер | ||
| Средняя скорость | Вейбулла, логнормальное, гамма-распределение | |
| Экстремальная скорость | Гумбеля, Вейбулла | |
| 6. Продолжительность солнечного сияния | Гамма-распределение | |
| 7. Комплекс температура—относительная влажность | Двумерное логнормальное | |
| 8. Комплекс температура—скорость ветра. | Моргенштерна — Гумбеля |
 2015-10-22
2015-10-22 4482
4482
