Оценка согласия между эмпирическим и теоретическим распределениями

В результате обработки данных наблюдений получают эмпирическую кривую распределения, которая характеризует частоту раз личных значений исследуемой величины. Эмпирическая кривая распределения всегда получается на основании ограниченной числа наблюдений, и, как правило, не позволяет объективно судить о законе, которому подчиняется распределение генеральной совокупности значений изучаемой величины.

Для установления этого закона обычно вводится предположение (гипотеза), что статистический ряд, лежащий в основе эмпирического распределения, представляет собой случайную выборку из генеральной совокупности, имеющей закон распределения f(x). Параметры этой функции, являющейся теоретическим законом распределения, как уже говорилось, вычисляют по данным наблюдений. Естественно, что между эмпирическим и теоретическим рядами распределения всегда будет некоторое расхождение.

Возникает вопрос, можно ли это расхождение считать несущественным, имеющим случайный характер, обусловленный ограниченным объемом выборки, или же оно является существенным и противоречит гипотезе, согласно которой данный статистический ряд можно рассматривать как выборку из генеральной совокупности с принятым теоретическим законом распределения.

Задача, таким образом, сводится к тому, чтобы установить, носит ли расхождение между выборочным и генеральным распределением случайный характер или нет.

Для решения указанной задачи необходимо, прежде всего, выбрать меру расхождения z между теоретическим и эмпирическим рядами.

Различными авторами предложены разные меры расхождения. Пока рассмотрим этот вопрос в общей постановке.

На основании принятой гипотезы о случайном характере расхождения мера расхождения является случайной величиной, для которой может быть найден интегральный закон распределения

F(z) = P(Z≤z),

откуда

Р (Z > z) = 1 - Р (Z ≤ z) = 1 - F (z). (6.1)

Далее пользуются «принципом практической невозможности маловероятных событий».

Согласно этому принципу, событие, обладающее малой вероятностью, считается практически невозможным, и поэтому, если оно все же наблюдается, то это говорит о несостоятельности гипотезы, на основании которой была определена его вероятность.

Для практического применения указанного принципа нужно выбрать границу вероятности Р₀ такую, что события А с вероятностями, меньшими данной Р(А)≤Р₀, можно полагать маловероятными, т. е. практически невозможными. Величину Р_о называют уровнем значимости. Уровень значимости — это вероятность принять случайное расхождение за систематическое. Сам выбор величины уровня значимости является условным. Чаще всего принимают Р₀ = 0,05 = 5 %.

Задавшись определенным уровнем значимости Р₀, можно из формулы (6.1) определить соответствующее ему значение z₀ — такое, что вероятность величины Z оказаться большей, чем z₀, будет равна

P(Z>z₀)=l-F (z₀) = Р₀. (6.2)

Величина z₀ является границей критической области для случайной величины Z. Значения Z > z₀ имеют на основании формулы (6.2) вероятность, не большую, чем Р₀, т. е. при заданном уровне значимости являются практически невозможными появление должно расцениваться как опровержение принятой гипотезы.

Величину Z называют критерием согласия. Критическое значение критерия согласия при данном уровне значимости P₀ –величина z₀.

Существует ряд критериев согласия, основанных на изучении распределения различным образом составленной меры расхождения.

Ни один из критериев согласия не может рассматриваться как достаточный, так как в его основе лежит условно установление мера расхождения и известная условность в оценке практически невозможных событий. Поэтому обычно рекомендуется производить оценку, по крайней мере, по двум критериям согласия.

В практике наиболее широко используются критерии Пирсона и А. Н. Колмогорова.

За меру расхождения теоретического и эмпирического распределений Пирсон принимает величину , определяемую формулой

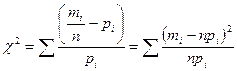(6.3)

Где n — объем совокупности, относительные частоты эмпирического распределения, p_i — соответствующие теоретические относительные частоты, вычисленные с помощью гипотетической функции распределения F(х) по формуле

p_i=F(x_i+1)-F(x_i)≈f(xi)Δx

Для случайной величины χ был найден интегральный закон распределения F:

(6.4)

Интегральная функция F оказалась зависящей не только от: χ₀², но и от параметра g, называемого числом степеней свободы распределения.

Это число степеней свободы g зависит от числа интервалов в ряде распределения и числа дополнительных условий (связей), наложенных на ряды частот.

Если между теоретическим и опытными рядами частот не существует никаких соотношений, кроме единственного условия, что

где s — число градаций.

Если между теоретическими и опытными частотами существуют некоторые дополнительные связи, число которых равно , то g = s-1- .

Так, например, если производится сравнение опытного ряда с теоретическим рядом частот, вычисленных по нормальному закону распределения, и параметры этого нормального закона и а не определялись по опытным данным, то g = s— .

Если же параметры нормального закона и σ вычислялись по опытным данным, как это обычно и имеет место, то этим самым устанавливаются два дополнительных соотношения между опытными частотами и теоретической функцией распределения (а значит, и теоретическим рядом частот).

Следовательно, в этом случае = 2 и g = s— 3.

Зная вид функции Пирсона F(χ₀², g) и задавая различное число степеней свободы g и различные уровни значимости Р₀, можно вычислить соответствующие им значения χ₀². На практике χ₀² определяют с помощью специальных таблиц, например, табл. 6.1.

Таблица 6.1 Критерий согласия χ₀² (допустимые пределы величины χ²)

р0	g
0,10 0,05 0,01 0,001	2,7 3,8 6,6 10,8	4,6 6,0 9,2 13,8	6,2 7,8 11,3 16,3	7,8 9,5 13,3 18,5	9,2 11,1 15,1 20,5	10,6 12,6 16,8 22,5	12,0 14,1 18,5 24,3	13,4 15,5 20,1 26,1	14,7 16,9 21,7 27,9	16,0 18,3 23,2 29,6

Величина χ₀² является тем допустимым пределом, переходить который не должна величина χ², так как значения χ² > χ₀² имеют малую вероятность (меньшую, чем P₀). Если же такие значения получаются в результате расчетов по формуле (6.3), то это указывает на очень малую вероятность того, что расхождение между теоретическим и эмпирическим распределениями носит случайный характер. Поэтому принятая гипотеза о случайном характере расхождения должна быть отвергнута.

Б табл. 6.1 приведены значения допустимых величин при различных степенях свободы g и уровнях значимости Р₀.

Задавшись величиной уровня значимости P₀, можно определить из таблицы при данном g критерий согласия χ₀². Если χ², вычисленное по формуле (6.3), окажется равным или большим, чем χ₀², то это будет указывать на отсутствие согласия между эмпирическими и теоретическим распределениями.

Приведем пример оценки согласия между эмпирическим и теоретическим рядами частот (табл. 6.2). Выясним, подчиняется ли эмпирическое распределение нормальному закону.

Число градаций s = 9. Так как при определении теоретической функции распределения в виде нормального распределения, параметры этой кривой и σ определялись по опытному распределению, то число связей = 2. Следовательно, число степеней свободы g = 9 — 2—l=6. Задавшись уровнем значимости, например, P₀= 0,05, находим по табл. 6.1, что χ₀²,= 12,6. Так как вычисленное χ²,=7,16< 12,6, то полученное расхождение не противоречит гипотезе о случайном несущественном характере этого расхождения.

Таблица 6.2

Градация	Эмпирическая	Теоретическая	(mi-npi)²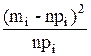
величины, х	частота mi.	частота npi-
Ниже 154				1,28
154—158				0,71
158—162				0,08
162—166				1,05
166—170				1,48
170—174				0,12
174—178				0,45
178-182				0,71
Выше 182				1,28
Всего			—	7,16

При применении критерия χ² необходимо, чтобы число n частоты т были достаточно большими. Если второе условие не выполняется, то необходимо укрупнить интервалы, т. е. произвести новую группировку.

А. Н. Колмогоров предложил другой критерий согласия, который в отличие от критерия Пирсона основан на сравнении интегральных законов опытного и теоретического распределений.

Пусть x₁, x₂, x₃..., х_n представляют результаты независимых наблюдений над случайной величиной X и пусть функция F*(x) = Р(Х<х) представляет эмпирический интегральный закон распределения X (функцию накопленных частостей эмпирического распределения). Необходимо выяснить, согласуется ли с этими данными предположение, что рассматриваемая случайная величина имеет некоторую непрерывную интегральную функцию F(х).

Составим абсолютные значения разности для разных значений х_i данного опытного распределения. Очевидно, что при идеальном совпадении теоретического и эмпирического законов распределения .

В качестве меры расхождения А. Н. Колмогоров использует величину

(6.5)

где n — объем совокупности, D — соответствует верхней границе (наибольшему значению 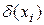) (рис. 6.1).

Согласно теореме Колмогорова, для различных уровней значимости Р₀ можно рассчитать те значения λ₀, которые не должна превышать полученная из опыта величина λ (табл. 6.3).

Практическое применение критерия λ для оценки степени близости экспериментального и теоретического распределений сводится к следующему.

Задавшись уровнем значимости Р₀, по табл. 6.3 определяют критерий согласия λ₀. Затем вычисляют по данным теоретического и статистического рядов величины 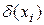и определяют из них наибольшую [D =.max ].

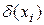Таблица 6.3

Критерий согласия λ₀ (допустимые пределы величины при различных уровнях значимости P₀)

р0%	99,9							0,1
λ0	0,374	0,520	0,571	0,828	1,224	1,358	1,627	1,950

Умножая ее на , находят . Если найденное таким образом λ окажется больше λ₀, то при данном уровне значимости гипотеза должна быть отвергнута и расхождение признано существенным. В противном случае, если λ<λ₀, можно считать, что между эмпирическим и теоретическим распределением существует удовлетворительное согласие.

При использовании этого критерия на практике рекомендуется брать уровень значимости Р₀ = 0,05 = 5 %.

Пример расчета. При анализе 225 измерений получено D = 0,08. Тогда λ = 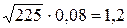= 1,2. Из табл. 6.3 следует, что на 5 %-ном уровне значимости λ₀ = 1,358. Так как λ < 1,358, то можно считать, что теоретическое и экспериментальное распределения согласуются на 5 %-ном уровне значимости.

Критерий А. Н. Колмогорова вычисляется значительно проще, чем критерий Пирсона. Однако, строго говоря, его можно применять лишь в тех случаях, когда известны параметры теоретического распределения, с которым проводится сравнение данного эмпирического распределения. Так как на практике чаще всего параметры вычисляются по эмпирическому распределению, то рассчитываемая по формуле (6.5) величина λ обычно оказывается заниженной. Таким образом, можно прийти к выводу, что данное: эмпирическое распределение хорошо согласуется с теоретическим хотя в действительности такого согласия может и не быть.