Климатические (статистические) характеристики распределений

Климатическими показателями, или характеристиками, принято называть обобщающие характеристики рядов многолетних наблюдений за метеорологическими величинами и явлениями, выражающие в компактном виде наиболее важные свойства распределений.

Климатические характеристики облегчают анализ и сравнение между собой метеорологических рядов.

Статистические распределения, представленные в дифференциальной форме, могут отличаться следующими свойствами: разным уровнем, т. е. центральными значениями, вокруг которых группируются все остальные наблюденные значения, разными амплитудами рассеяния наблюдавшихся значений вокруг центрального, различной асимметричностью и крутостью кривых распределений. Каждая из этих особенностей имеет свою количественную характеристику.

Особенно важны меры двух первых особенностей распределения. Статистической характеристикой первой из них являются средние величины, второй — дисперсия, среднее квадратическое отклонение или коэффициент вариации, а мерами третьей и четвертой особенностей служат коэффициенты асимметрии и эксцесса.

Наиболее часто используемой мерой средней или центральной величины является среднее арифметическое, определяемое следующим образом:

(3.1)

Для сгруппированных данных (т. е. если вместо ряда имеется статистическое распределение) делается допущение, что значения сгруппированы в центре каждой градации и поэтому осредняются середины интервалов, умноженные на частоту градаций, т. е.

(3.2)

где — середина градации,

или

(3.3)

Среднюю арифметическую, получаемую по одной из двух последних формул, часто называют взвешенной средней арифметической, подчеркивая тем самым, что она вычислена с учетом частот , характеризующих весомость данной градации в общей сумме всех членов совокупности. Чем больше вес, с которым входит какая-либо градация в формулу (3.3), тем сильнее влияние срединного значения этого интервала на окончательный результат.

Числовые значения одного и того же ряда, получаемые по формулам (3.1) — (3.3), вообще говоря, должны быть одинаковыми. Однако на практике между ними обычно всегда имеется некоторое различие, так как последние формулы дают приближенный результат, поскольку все значения х в каждой градации приравниваются к ее середине.

В климатологии чаще всего вычисляют средние по срокам, средние суточные, декадные и месячные. Целесообразно подсчитывать средние за больший период по средним за меньший. Например, среднее за год подсчитывается как среднее арифметическое средних величин за 12 месяцев, а среднее месячное на основе средних в сроки наблюдений.

Следует иметь в виду, что в некоторых странах средние суточные значения вычисляются по трехсрочным наблюдениям или даже как среднее из показаний максимального и минимального термометров (среднее из этих двух температур осредняется во времени). Такие средние могут систематически отличаться от средних, полученных по ежечасным и срочным значениям, что надо помнить при сопоставлении данных разных станций.

Если дифференциальное распределение симметричное и одновершинное, то в интервал, включающий среднее, попадает наибольшее число членов ряда, а среднее делит ряд на две равные части: значений, больших и меньших среднего. Ориентируясь на эти свойства, иногда ошибочно считают, что среднее значение наблюдается наиболее часто. Даже при одновершинном симметричном распределении само среднее значение может наблюдаться редко или вообще не встречаться (например, нецелое среднее число дней в месяце с грозой или с другим явлением). В таких случаях правильно говорить, что в половине случаев наиболее часто (но далеко не «почти ежегодно») встречаются значения, близкие к среднему.

Полезно постоянно иметь в виду, что сумма отклонений от среднего равна нулю

Это иногда используется для контроля правильности определения . Если определено для некоторого периода наблюдений, а в дальнейшем появляются систематические (одного знака) отклонения от среднего, то это служит первым сигналом нарушения однородности.

Для несимметричных и неодновершинных распределений используют и другие меры уровня ряда — моду и медиану.

Мода Мо — это наиболее часто встречающееся значение в ряду. Мода полезна при описании уровня распределений числа дней с явлением, направления ветра и для других резко асимметричных распределений.

В качестве приближенного значения моды можно использовать середину интервала, на который приходится наибольшая повторяемость. Ценность знания моды вытекает из ее определения: именно это и близкое к нему значение (а не среднее) наблюдается наиболее часто. Однако полезность моды ограничена, так как она не может в силу своих свойств использоваться для дальнейшего анализа и не участвует в расчетах.

Медиана Me делит совокупность упорядоченных данных на две группы одинакового размера. Она является средним членом ранжированного ряда при нечетном числе членов ряда и средним из двух срединных членов ряда при четном числе членов. Медиана является 50 %-ной квантилью.

Медиану целесообразно использовать, когда крайние значения определены недостаточно надежно, что может привести к существенной ошибке в средней. Медиана используется и тогда, когда отдельные наблюдения не дают определенных значений. Например, при рассмотрении ряда лет образования устойчивого снежного покрова, возможно, что в некоторые зимы устойчивый снежный покров не образовывался. В этом случае следовало бы определять медиану ряда, относя зимы с отсутствием снежного покрова к числу членов ряда с более поздними датами. Это и будет такая характеристика, что в половине лет устойчивый снежный покров образовывался до, а во второй половине — после этой даты (или не образовывался). Полезно также помнить, что медиана представляет собой значение, сумма абсолютных отклонений членов ряда от которого наименьшая:

Самой простой мерой рассеяния данных вокруг среднего значения является амплитуда, т. е. разность наибольшего и наименьшего значений ряда. Например, годовая амплитуда средней температуры воздуха представляет собой разность между средней суточной температурой воздуха самого теплого и самого холодного месяцев. Используется иногда среднее абсолютное отклонение, т. е. среднее из модулей отклонений отдельных значений от среднего.

Чаще всего в качестве меры рассеяния принимается среднее квадратическое отклонение а, которое вычисляется по формулам

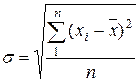(3.4)

(3.5)

(3.6)

Логика выбора одной из этих формул та же, что и при выборе формулы для расчета средней. Преобразуя любую из этих формул, получаем еще одно выражение

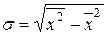(3.7)

Среднее квадратическое отклонение не может быть отрицательным. Квадрат среднего квадратического отклонения носит название статистической дисперсии D, которая является аналогом теоретической дисперсии.

Кроме перечисленных характеристик рассеяния для метеорологических величин, средние значения которых в разных районах могут сильно различаться (количество осадков, высота снежного покрова, скорость ветра, продолжительность солнечного сияния), для устранения влияния величины среднего используется относительная характеристика — коэффициент вариации

(3.8)

Мерой асимметрии (скошенности) распределения служит коэффициент асимметрии, вычисляемый по формулам

(3.9)

(3.10)

(3.11)

Преобразуя любую из этих формул (возводя разности в куб), получим выражение

(3.12)

Коэффициент асимметрии может принимать как отрицательное, так и положительное значение и равен нулю при симметричном распределении.

Когда наблюдается правосторонняя асимметрия распределения, т. е. удлиненной является правая ветвь кривой дифференциального распределения, сумма кубов положительных отклонений от средней больше суммы кубов отрицательных отклонений

и поэтому А>0. В этом случае Мо<Ме< .В случае левосторонней асимметрии больше сумма кубов отрицательных отклонений А < 0. В этом случае < Me < Mo.

Асимметричность распределения принято считать малой при , умеренной при 0.25< и большой при . Этими критериями пользуются при подборе клетчатки, спрямляющей распределение.

В качестве меры крутости (островершинности) распределения используется коэффициент эксцесса, вычисленный по формулам (3.13) 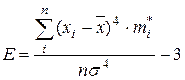(3.14) 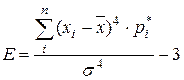(3.15)

а также по формуле, полученной после преобразования любой из этих формул: 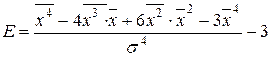(3.16)

Коэффициент эксцесса может принимать значения в диапазоне от —2 до ∞. При Е = — 2 кривая распадается на две отдельные кривые.

Крутость кривой с помощью величины Е оценивается по сравнению с одной из наиболее часто используемых на практике теоретических кривых распределения — кривой нормального распределения. При E<0 кривые менее островершинны, чем нормальные, при E>0, наоборот.

Принято считать эксцесс малым, если ≤0.5, умеренным, если 0,5< ≤1,0 и большим при >1,0.

Зная, Mo, Me, σ, А и Е, можно делать определенные заключения о распределении членов ряда. Если известно, что ряд хорошо описывается нормальной кривой (см. табл. 5.7; A и E примерно равны нулю), то в пределах ±σ лежит 68% наблюдений в пределах ±2σ— примерно 95%, а в пределах ±3σ -99,7 %. Вообще же при любом виде кривой распределения в пределах ±2σ находится 75 % всех измерений, а в пределах ±3σ- 89 %. Если распределение симметрично (A≈0), а E>0, то вблизи среднего значения группируется большое (большее, чем при нормальном) количество наблюдений, но сравнительно велико (несколько процентов) и число наблюдений за пределами Зσ. При Е < 0 наоборот: вблизи наблюдений меньше, но практически все они лежат в пределах ±3σ.

Характеристики , σ, А и Е иногда называют «моментными», так как они объединены общим понятием моментов разных порядков.

Начальными моментами v называют средние из значений величины, возведенных в ту или иную степень

(3.17)

Или

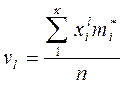(3.18)

Центральные моменты —это средние из отклонений отдельных значений от среднего, возведенных в разную степень:

(3.19)

(3.20)

Легко видеть, что при l =1 является средним арифметическим, — средним квадратическим отклонением, а μ₃ и μ₄— пропорциональны коэффициентам асимметрии и эксцесса (точнее E+3).

Необходимо остановиться на одном частном примере — подсчете среднего числа случаев (или дней) с редким явлением, которое наблюдается не ежегодно. Возможны два подхода. Подсчитывается общее число случаев (дней) и делится на общее число лег (в годы, когда явление не наблюдалось, число случаев или дней считается равным нулю). Это среднее ₁ вполне соответствует данному выше определению, а по смыслу предполагает, что наблюдение нескольких случаев в одном году случайно, и они «с таким же успехом» могли достаточно равномерно распределиться по всем годам. Но именно это соображение во многих случаях несправедливо. Часто несколько случаев (несколько дней с явлением) в одном году обусловлены одной крупномасштабной (по времени и пространству) синоптической ситуацией. Считать эти события независимыми нельзя и неоправданно распределять их равномерно по всем годам. Если случаи с явлением не разделены большим временным промежутком, то решить вопрос об их связанности довольно сложно.

Второй подход: определяется среднее число случаев (дней) ₂ только в годы наличия явления (делится на число лет, когда явление наблюдалось) _ и дается еще одна характеристика — процент (доля) лет Р, когда наблюдалось явление (отношение числа лет с явлением к общему числу лет). Очевидно, ₁ =P _2. Второй подход свободен от указанного выше недостатка. Информация оказывается более полной и точнее соответствует реальной ситуации. Но если случаи с явлением действительно независимы, то для ₁ можно пользоваться распределением Пуассона {см. ниже), а для ₂, которое по самому смыслу («среднее в годы наличия явления») не меньше единицы, — нельзя, а надо вначале перейти к _1.

Климатические показатели двумерного распределения значительно более многообразны и многочисленны. Таковыми служат, прежде всего, характеристики каждой из одномерных величин, являющихся компонентами двумерной (т. е, , σ_х, А_х, Е_х и , σ_у, А_у, Е_у). Кроме этих характеристик в случае двумерного распределения необходимо ввести еще характеристики связей между компонентами двумерной величины.

Наиболее важной из них является коэффициент корреляции, который служит мерой тесноты прямолинейной связи между величинами, составляющими комплекс, и вычисляется по формулам

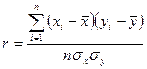(3.21)

(3.22)

(3.23)

Коэффициент корреляции может принимать значения от -1 до +1; он уменьшается по своей абсолютной величине по мере ослабления линейной корреляционной связи.

Рис. 3.1. Корреляционный график.

Для того чтобы создавалось ясное представление о смысле коэффициента корреляции, прежде всего следует определить само понятие корреляционной связи.

Между переменными величинами могут наблюдаться два вида связи: статистическая и функциональная, которые принципиально различаются между собой.

В случае функциональной связи каждому из рассматриваемых значений переменной х соответствует вполне определенное (иногда не одно) значение y.

В случае статистической связи всякому заданному значению соответствует не одно значение у, а распределение значений у, изменяющееся вместе с изменением х, и наоборот, каждому заданному значению у соответствует множество значений х. Такие связи могут существовать и между более чем двумя величинами.

Пусть имеются данные наблюдений за двумя величинами х и у. Если между ними существует статистическая зависимость, то результаты наблюдений, представленные на графике в виде точек, расположатся на поле графика подобно тому, как это показано на рис. 3.1. Несмотря на кажущуюся хаотичность в расположении точек, обращает на себя внимание хорошо заметная тенденция возрастания одной величины при увеличении другой.

Чтобы получить возможность объективной оценки данной статистической зависимости, разобьем весь диапазон значений х и у на отдельные градации и получим вертикальные и горизонтальные строки, аналогичные столбцам и строкам таблицы двумерного распределения.

Для каждого вертикального столбца х вычислим среднее значение у, которое обозначим . Эта величина носит название условной средней Y по X. Можно свести в таблицу условные средние (табл. 3.1), а на графике соединить условные средние отрезками прямой.

Таблица 3.1

Эмпирическая регрессия Y по X

Значения хi	x1	x2	x3	x4	x5	x6	x7
Условные средние ухi	yx2	yx3	yx4	yx5	yx6	уx7

Аналогично для каждой горизонтальной строки У можно вычислить условные средние и построить таблицу и график.

Обычно говорят, что таблицы, подобные приведенной выше, характеризуют эмпирическую регрессию У по X или аналогично Z пo Y.

Анализ рис. 3.1 позволяет сделать вывод, что при возрастании величины X (или У) соответствующие значения У (или X) в отдельных наблюдениях могут и увеличиваться и уменьшаться. Тем не менее, средние значения одной величины, соответствующие значениям другой, обнаруживают известную зависимость от значений второй величины. Такой характер статистической связи носит название корреляционной связи.

Линии эмпирической регрессии на графике (ломаные линии могут быть выровнены методом наименьших квадратов) пересекаются в точке с координатами, равными средним значениям X и У (, ).

Степень близости корреляционной зависимости к функциональной характеризует угол между линиями регрессии X по У и У по X. При функциональной связи две кривые сливаются.

Уравнение линий регрессии можно представить в виде

(3.24)

(3.25)

Можно показать, что ρ_у/х и ρ_x/у являются тангенсами углов наклона линий регрессии по отношению к осям координат, которые они пересекают, и могут быть записаны в виде

(3.26)

(3.27)

Тангенс угла между линиями регрессии зависит от коэффициента корреляции. Если этот угол обозначить ψ, то

(3.28)

Строго уравнение линии регрессии строится по методу наименьших квадратов; сумма квадратов отклонений ординат точек от линии должна быть наименьшей. Уравнение такой линии имеет вид

(3.29)

и линия эта проходит через точку (, ). Обычно линию проводят через точки (, ) и (0, , ). Линия регрессии заменяет статистическую связь функциональной и позволяет с определенной погрешностью определять неизвестное значение y_k при заданном x_k- Поскольку истинная связь не функциональная, то при заданном x_k величина y_k. может принимать различные значения. Ошибка их замены значением y_k, определенным по уравнению (3.29), составляет

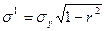(3.30)

и ориентировочно можно считать, что в пределах у_k ± 2σ' укладывается около 70% действительных значений у, наблюдающихся при x_k. Чем ближе r к единице, тем уже соответствующая полоса: например, для r = 0,92 она составляет 0,4σ_у, а для r= 0,6 — 0,8σ_у. Если считать, что при всех x_ky_k = , то ошибка составляет σ_у. Таким образом, использование уравнений регрессии при r > 0,8 позволяет уменьшить ошибку определения y_k примерно вдвое.

Положительным значениям r соответствует прямая корреляционная зависимость, т. е. при возрастании (убывании) одной из величин, другая в среднем также возрастает (убывает); отрицательным значениям г соответствует обратная корреляционная зависимость, т. е. возрастание одной величины соответствует в среднем убыванию другой, и наоборот.

На рис. 3.1 представлена прямая корреляционная связь.

На практике принято считать, что величины достаточно тесно связаны между собой, если |r|>0,7 или даже |r|>0,6. Однако всегда следует осторожно относиться к заключениям, основанным на значении коэффициента корреляции. В некоторых случаях нельзя категорически говорить о наличии зависимости даже при |r|= 0,9, если она не может быть объяснена физическими соображениями.

Отсутствию корреляционной линейной связи соответствует r = 0, однако из-за ограниченности используемых рядов и связанных с этим ошибок и в этом случае получается некоторое значение r, отличное от нуля. При нормальном распределении с вероятностью 95 % можно утверждать, что коэффициент корреляции значимый (т. е. связь существует) при следующих значениях r и числах пар N:

N
i	0,42	0,36	0,20	0,15

Следует иметь в виду, что если r≈0, то это еще не означает, что связи нет. Нередко между исследуемыми величинами связь имеет место, но она носит нелинейный характер, в этом случае малые значения коэффициента корреляции еще не говорят об отсутствии связи, так как следует помнить, что r характеризует степень тесноты лишь линейной зависимости между случайными величинами.

Для оценки степени нелинейной корреляционной связи в статистике принято вычислять корреляционное отношение. Однако здесь формулы корреляционных отношений мы не приводим, так как в климатологической практике эта характеристика не имеет широкого применения. Нелинейная связь между метеорологическими элементами обычно не бывает тесной. А в случае нелинейности связи ее учет не имеет практического смысла, так как уточнение тесноты связи за счет нелинейности меньше погрешности расчета характеристики связи (корреляционное отношение отличается от коэффициента корреляции меньше, чем на величину ошибки того и другого).

Часто рассматривается корреляционная связь между значениями одной и то же величины в различные моменты времени.

В общем случае из многолетнего ряда наблюдений берут N одинаковых временных отрезков (например, январей), в каждом из них значения членов нумеруют. Выражение для коэффициента корреляции между i-м и j-м членами записывается в виде

При изменении i и j изменяется и r, которое в этом случае называется корреляционной функцией. Эта функция симметрична (r_ij = r_ji)> поэтому можно ограничиться значениями j > i

Если процесс изменения рассматриваемой величины стационарен, т. е. представляет собой случайные колебания около некоторого среднего, амплитуда и характер которых не меняются существенно с течением времени, то r осредняется для всех разностей l = j - i, имеющих одинаковое значение. В качестве аргумента такой осредненной корреляционной функции рассматриваются или разность номеров l или соответствующий сдвиг во времени τ.

Корреляционные функции используются как для оценки инерционности атмосферных процессов, так и в различных климатических расчетах, в частности, при получении одной климатической характеристики по другим, при косвенном вычислении статистических характеристик комплексов метеорологических величин, при оценке ошибок статистических характеристик (см. ниже).

Более полный набор характеристик двумерного распределения можно получить, рассматривая характеристики асимметрии и эксцесса двумерного распределения. Их описание можно найти в работе [3].