Функциональные клетчатки и их использование в климатологии

Для анализа статистических распределений и графического определения ряда статистических характеристик во многих случаях удобно применять специальный бланк с функциональной координатной сеткой. На таком бланке одна из шкал или обе являются неравномерными. Это объясняется тем, что на шкале откладываются не значения величины, а значения той или иной функции от нее. Поскольку значения функции откладываются в равномерной шкале, а оцифровка выполняется в виде значений не функции, а самой величины, для последней шкала оказывается неравномерной. Например, строится равномерная шкала для логарифма х, на ней откладываются значения логарифма для целых-значений х через 1. Естественно, что эти значения х будут отстоять друг от друга на разных расстояниях. Образуется неравномерная шкала.

Наиболее употребительны в климатологии функциональные сетчатки: нормальная («вероятностная бумага»), Вейбулла, Гумбеля, логнормальная. На этих клетчатках интегральные кривые соответствующих распределений превращаются в прямые линии. Благодаря этому появляется возможность экстраполяции распределения в область редких значений метеорологической величины, т.е. решается чрезвычайно важная прикладная задача. Кроме того, использование клетчатки часто помогает упростить получение параметров распределения.

Для того чтобы построить клетчатку, следует найти некоторую функцию от метеорологической величины или ее вероятности, которая была бы линейно связана в первом случае с вероятностью, во втором — с величиной. Это делается исходя из физических соображений или из вида кривой распределения. Возможен так же графический путь определения и построения функциональной шкалы. Последний путь возможен применительно к тем законам распределения, которые представлены в табличной форме в зависимости от их статистических характеристик.

Схема графического построения клетчатки вероятности (в данном примере «нормальной») представлена на рис. 8.1. По тому принципу могут быть построены и другие клетчатки (рис. 8). Однако следует помнить, что в одном случае преобразуется шкала вероятностей (см. рис. 8.1), а в других случаях возможно преобразование шкалы самой величины (см. рис. 8.2).

Рассмотрим более подробно построение некоторых клетчаток. Наиболее важной из них является вероятностная бумага, на которой интегральная кривая нормального распределения преобразуется в прямую линию.

Пусть мы имеем функцию нормального распределения величины х, F(х) величины F и F'(t).

При этом для заданной вероятности P_<x = F(x) и Р_<t =F(t) квантили величин х и Т связаны между собой соотношением

(8.1)

или

(8.2)

Уравнение (8.1) в координатах х_Р и t_P является уравнением прямой линии, проходящей через точку с координатами х_Р= и t_P = 0, с угловым коэффициентами

Будем откладывать на вертикальной или горизонтальной с отрезки, пропорциональные значениям функции Т (являющее обратной функцией F(t), т. е. t_P = G(P_<t), надписывая у концов этих отрезков значения аргумента P_<xсоответствующие данным t_p.

Таким образом, при построении вероятностной бумаги использована функция от вероятности t_P, связанная линейно с величиной х, т. е. с х_р.

В качестве примера определим для t = — 2, —1, 0, 1 и 2 соответствующие значения Р_<t. Как указывалось ранее,

(8.3)

(8.4)

Тогда, определяя значения Ф₁(t) по таблице справочника, получим

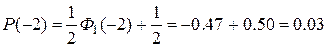
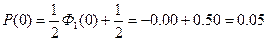
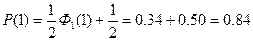
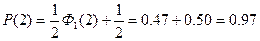
Отложив на оси клетчатки t_p = 0 отрезки, пропорциональные t_P = —2, t_P = —1, t_p = 0, и т. д., проставляем у их концов значения Р(—2)-0,03 или 3%, Р(—1) = 0,16 или 16%, Р(0) = 0,5 или 50 % и т. д. Так и построена вертикальная шкала вероятностной бумаги, изображенной на рис. 8.3.

С помощью вероятностной бумаги можно решать следующие задачи.

1.Определить, подчиняется ли данное статистическое распределение нормальному закону.

Признаками того, что статистическое распределение подчиняется нормальному закону, является расположение точек, построенных на вероятностной бумаге по данным о значении случайной величины X и статистическим значениям интегральной повторяемости , вдоль линии, близкой к прямой.

2.Графически определить параметры статистической совокуcности нормально распределенной случайной величины — среднее арифметическое и среднее квадратическое отклонение σ.

Если на вероятностной бумаге построена прямая линия, соответствующая нормальному распределению данной величины, то его средняя арифметическая отсчитывается на горизонтальной оси как 50%-ная квантиль, а модуль σ определяется как разность 50 и -16 %-ных квантилей (или 84 и 50%-ных квантилей). Это можно выразить следующим образом:

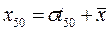
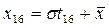
откуда

Или

Поскольку

Значит

3. Определить интегральную функцию распределения (обеспеченность) значений случайной величины, подчиняющейся нормальному закону, если известны параметры и σ.

Для этого достаточно построить на вероятностной бумаге прямую линию (см. рис. 8.3), проходящую через две точки: A(X = , Р = 50%) и В (X = -σ,Р = 16 %) и снять с графика вероятность любого значения случайной величины.

Клетчатка логнормального распределения строится на основе вероятностной бумаги, и лишь шкала значений метеорологической величины заменяется на неравномерную, логарифмическую. Вдоль этой оси откладывается логарифм целых значений величины X, а у концов отрезков, пропорциональных lgx, проставляются значения X.

Распространенным видом клетчатки являются клетчатки Вейбулла и Гумбеля (первого типа). На этих клетчатках строятся обычно распределения экстремальных величин. При этом на первую наносится вся совокупность наблюдений за метеорологической величиной, а на вторую — лишь годовые (или месячные) ее максимумы.

Функция распределения Вейбулла имеет вид

(8.5)

где F_≥x — интегральная вероятность, т. е. вероятность того, что значения величин больше х; β и γ -параметры распределения.

Распределение получено как частный случай известного распределения Гудрича, использованного уже рядом исследователей при описании некоторых распределений из области гидрологии и климатологии.

Уравнение (8.5) удобно решать графически. Тогда при определении вероятности больших значений X можно обойтись без знания параметров р и у.

В самом деле, прологарифмировав дважды соотношение (8.5),, найдем, что

(8.6)

Выражение (8.6) является линейным относительно lgx и lg(-lgF). Поэтому если на прямоугольную координатную сетку в системе координат lgx и lg(-lg F) нанести точки, полученные по данным материалов многолетних наблюдений, то точки эти
должны лечь на одну прямую при условии, что уравнение (8,5) правильно выражает закон распределения. Продолжив эту прямую до заданного значения величины, легко снять с графика соответствующую этому значению вероятность F и установить тем самым, с какой вероятностью величина X превысит заданное значение. И наоборот, можно определить, на какое значение X следует рассчитывать при заданной вероятности.

Такой график представлен на рис. 8.4. На вертикальной оси графика отложены в логарифмическом масштабе значения X, на горизонтальной — интегральная вероятность (повторяемость) значений величины X в билогарифмическом масштабе. Данное распределение используется для расчетов максимальной скорости ветра.

Из вышеизложенного следует, что для определения максимальной скорости ветра при данном уровне вероятности Р необходимо:

1.По материалам наблюдений за некоторый ряд лет вычислить повторяемость (вероятность) различных градаций скорости ветра.

2.На основании этих данных вычислить интегральную вероятность F для нескольких значений скорости ветра и нанести соответствующие точки на график.

3.Провести прямую как можно ближе к нанесенным точкам и продолжить ее в область графика с большими значениями скорости ветра. На оси абсцисс отыскать соответствующее заданному уровню вероятности значение F = 100 — Р и снять с графика искомую максимальную скорость ветра.

Рассмотренный метод дает хорошие результаты при условии, что исходные данные о повторяемости ветра различной скорости получены на основании достаточно длинных рядов наблюдений. При вычислении месячных характеристик ветра желательно использовать ряды длительностью в 15—20 лет. Если такие ряды отсутствуют, то лучше производить расчет характернее ветра по сезонам. В последнем случае достаточны ряды в 8-10 лет.

Клетчатка Гумбеля близка к клетчатке Вейбулла, но не совпадает с ней, так как на ее оси откладывается не вероятность значений, больших или равных заданной, а меньших заданной, т.е.1 — F_≥x.

На ось наносятся значения у_р, при этом ось вероятностей преобразуется в неравномерную, а ось скорости ветра строится в линейном масштабе.

Строятся и другие клетчатки, например, нормальная для кубов значений метеорологических величин. Некоторые законы, например, биномиальный и композиционные, представляются набором клетчаток для разных параметров.

Часто на вероятностную клетчатку наносят данные имеющегося статистического ряда для того, чтобы подобрать подходящую (желательно спрямляющую) линию — график функции распределения.

При этом бывает полезно объединить несколько пунктов наблюдений, что удлиняет ряд и уменьшает роль случайных ошибок. Для исключения систематических различий в таких случаях целесообразно в качестве переменной использовать не х, а отношение х/ или разность (х — ). Использование отношения при объединении пунктов может быть подходящим для скорости ветра, непрерывной продолжительности атмосферных явлений или заданных значений метеорологических величин, использование разности — для температуры.

При таком подходе во многих случаях точки разных пунктов ложатся в одну группу и линия получается более обоснованной. На заключительном этапе для каждого пункта, зная , переходят от х/ к х или от (х — ) к х. Например, если получилось, что Р(х/ <5)=0,3, то для пунктов с = 3 и = 6 это соответственно будет P₁ (x₁ < 15) =0,3 и Р₂(х₂ < 30) =0,3.