Пусть некоторая центральная база снабжает продукцией (ее можно считать однородной) m складов. Развозка продукции на склады осуществляется одним грузовиком, причем каждый склад получает свой заказ полностью в один прием –грузоподъемность грузовика для этого достаточна. Вообще же грузовик может одновременно взять груз, соответствующий не более чем  заказам. Грузовик может объезжать склады по определенным r маршрутам. Разумеется, один и тот же склад может находиться на разных маршрутах.
заказам. Грузовик может объезжать склады по определенным r маршрутам. Разумеется, один и тот же склад может находиться на разных маршрутах.
Пусть для каждого склада известна функция затрат по доставке в зависимости, скажем, от размера заказа. Требуется составить график развозки, обеспечивающий всех клиентов и минимизирующий суммарные затраты. Подчеркнем, что время доставки здесь никак не учитывается; предполагается, что все операции по доставке заведомо могут быть осуществлены в течение некоторого периода времени, устраивающего всех заказчиков.
Под способом развозки будем понимать любую допустимую комбинацию выполнения заказов. Говоря точнее, способ развозки представляет собой  -мерный столбец,
-мерный столбец,  -я компонента которого равна единицы, если
-я компонента которого равна единицы, если  -й заказ в этом способе удовлетворяется, и равна нулю в противном случае. Для любой реальной задачи при небольших значениях
-й заказ в этом способе удовлетворяется, и равна нулю в противном случае. Для любой реальной задачи при небольших значениях  можно фактически выписать все такие способы развозки. Число
можно фактически выписать все такие способы развозки. Число  этих способов будет зависеть не только от этих параметров, но и, например, от числа складов на каждом маршруте, объема заказов и так далее. Кроме того, каждому способу развозки
этих способов будет зависеть не только от этих параметров, но и, например, от числа складов на каждом маршруте, объема заказов и так далее. Кроме того, каждому способу развозки  легко сопоставить связанные с ним затраты
легко сопоставить связанные с ним затраты  (учитывающие, помимо упомянутых выше затрат по доставке, также стоимость работ по выгрузке и тому подобное).
(учитывающие, помимо упомянутых выше затрат по доставке, также стоимость работ по выгрузке и тому подобное).
Итак, пусть при данных конкретных условиях задачи составлена матрица  всевозможных способов развозки, состоящая из нулей и единиц. Столбцы этой матрицы представляют собой описанные выше способы развозки, то есть
всевозможных способов развозки, состоящая из нулей и единиц. Столбцы этой матрицы представляют собой описанные выше способы развозки, то есть 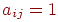 , если в способе
, если в способе  заказ
заказ  удовлетворяется, и
удовлетворяется, и  в противном случае. Кроме того, пусть для каждого способа
в противном случае. Кроме того, пусть для каждого способа  найдены соответствующие ему затраты
найдены соответствующие ему затраты  . Теперь задача состоит в выборе наиболее экономичной комбинации этих способов.
. Теперь задача состоит в выборе наиболее экономичной комбинации этих способов.
Введем переменные

| (7.15) |
Теперь мы естественным образом получаем задачу минимизации суммарных затратт
 (7.16.)
(7.16.)
при условиях (7.15.) и
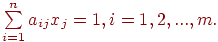
| (717) |
Условия (7.17.) означают, что все заказы должны быть удовлетворены.
Обращаем внимание на то, что модель (7.15.)-(7.17.) физически совпадает со взвешанной задачей о покрытии.
 2015-10-22
2015-10-22 333
333








