Распределительная задача с фиксированными доплатами

Пусть в дополнение к перечисленным выше данным выпуск транспортной единицы типа на линию связан с подготовительными работами, требующими времени (это время не зависит от числа рейсов, которое предстоит выполнить данной транспортной единице). Денежные затраты на проведение этих подготовительных работ составляют .

Для отыскания наиболее экономной расстановки транспортных единиц по линиям, как и выше, введем целочисленные переменные . Тогда суммарные затраты составят

(7.7)

где

(7.8)

Ограничения по фонду времени каждой транспортной единицы будут теперь иметь вид

(7.9)

где

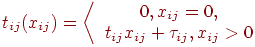
(7.10)

Ограничения по рейсам (7.4.), равно как и очевидные ограничения (7.2.), при этом сохраняются. Таким образом, задача заключается в минимизации (7.7.) при условиях (7.2.), (7.4.) и (7.9.)

Из (7.7.) и (7.8.) легко усмотреть, что перед нами задача с фиксированными доплатами; ее отличие от рассматривавшихся ранее задач этого рода состоит в том, что здесь фиксированные доплаты входят не только в целевую функцию, но и в ограничения (7.9.). Однако и этот вариант задачи можно свести к целочисленная задача линейного программирования.