Расчёт прочности:
При изучении явления удара принимаем следующие ограничения и допущения:
1. В ударяемой конструкции возникают напряжения, не превосходящие предела пропорциональности, и закон Гука при ударе сохраняет свою силу.
2. Удар является неупругим, и после удара тела не отделяются друг от друга.
3. Ударяющее тело является абсолютно жёстким и не деформируется.
4. Сопротивлением движению пренебрегаем.
5. Масса ударяемой конструкции мала по сравнению с массой ударяющего тела и в расчёт не принимается.
Определение напряжений и деформаций при ударе производится на основании закона сохранения энергии.
Пусть груз  без начальной скорости падает на упругую конструкцию с высоты
без начальной скорости падает на упругую конструкцию с высоты 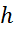 . Если пренебречь сопротивлением воздуха, скорость падения груза можно определить по формуле
. Если пренебречь сопротивлением воздуха, скорость падения груза можно определить по формуле 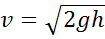 . Отсюда следует, что
. Отсюда следует, что 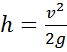 . Таким образом, всякий удар со скоростью
. Таким образом, всякий удар со скоростью 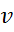 можно привести к свободному падению с условной высоты
можно привести к свободному падению с условной высоты 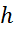 .
.
Наибольшая динамическая деформация при ударе в точке падения груза 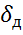 определяется по формуле:
определяется по формуле:
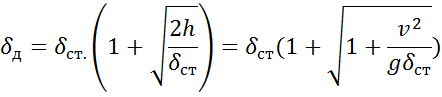
Величина в скобках показывает, во сколько раз динамическая деформация больше статической. Эта величина называется динамическим коэффициентом удара. Таким образом,
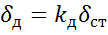 , где
, где 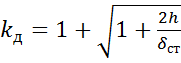 .
.
Так как по закону Гука напряжения пропорциональны деформациям, то  . Величина напряжений при ударе зависит от величины деформаций, т.е. от жёсткости ударяемого тела. С уменьшением жёсткости напряжения при ударе уменьшаются.
. Величина напряжений при ударе зависит от величины деформаций, т.е. от жёсткости ударяемого тела. С уменьшением жёсткости напряжения при ударе уменьшаются.
При мгновенном приложении нагрузки без удара 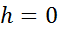 и из формулы
и из формулы 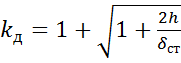 получим
получим 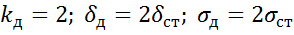
Если высота падения груза весьма велика по сравнению с  , то величина динамического коэффициента определяется по приближённой формуле:
, то величина динамического коэффициента определяется по приближённой формуле: 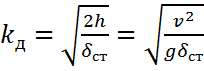
Условие прочности: 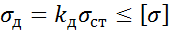
 2015-10-22
2015-10-22 909
909








